The theorem is named after R. Leonard Brooks, who published a proof of it in 1941. A coloring with the number of colors described by Brooks' theorem is...

all other cases, the bound can be slightly improved; Brooks' theorem states that Brooks' theorem: χ ( G ) ≤ Δ ( G ) {\displaystyle \chi (G)\leq \Delta...

combinatorial games, and the proofs of other mathematical results including Brooks' theorem on the relation between coloring and degree. Other concepts in graph...

exactly 1. By Brooks' theorem, any graph G other than a clique or an odd cycle has chromatic number at most Δ(G), and by Vizing's theorem any graph has...

In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than...

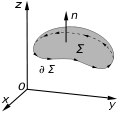
theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls, or simply the curl theorem,...

In database theory, the CAP theorem, also named Brewer's theorem after computer scientist Eric Brewer, states that any distributed data store can provide...

{\displaystyle n=k} vertices, or an odd-length cycle graph. This is Brooks' theorem. 2 m ≥ ( k − 1 ) n + k − 3 {\displaystyle 2m\geq (k-1)n+k-3} . 2 m...

single graph automorphism, the identity automorphism. According to Brooks' theorem every connected cubic graph other than the complete graph K4 has a...

{\displaystyle G} . When G {\displaystyle G} is not an odd cycle or a clique, Brooks' theorem states that the upper bound can be reduced to Δ ( G ) {\displaystyle...

vertices of the same color. It has a list coloring with 3 colors, by Brooks' theorem for list colorings. The Petersen graph has chromatic index 4; coloring...

The Zero Theorem is a 2013 science fiction film directed by Terry Gilliam, starring Christoph Waltz, David Thewlis, Mélanie Thierry and Lucas Hedges....

significantly greater than its equitable chromatic number of two. Brooks' theorem states that any connected graph with maximum degree Δ has a Δ-coloring...

theorem (proof theory) Deduction theorem (logic) Diaconescu's theorem (mathematical logic) Easton's theorem (set theory) Erdős–Dushnik–Miller theorem...

primarily focused on problems related to graph coloring, including work on Brooks' theorem, the Borodin–Kostochka conjecture, list critical graphs, and Read's...

In calculus, Taylor's theorem gives an approximation of a k {\textstyle k} -times differentiable function around a given point by a polynomial of degree...

He wrote a significant paper on the series of chromatic numbers and Brooks' theorem, titled Hajós graph coloring conjecture: variations and counterexamples...

In mathematics, specifically in real analysis, the Bolzano–Weierstrass theorem, named after Bernard Bolzano and Karl Weierstrass, is a fundamental result...

The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at every...

chromatic number 4. It has book thickness 3 and queue number 2. By Brooks’ theorem, every k-regular graph (except for odd cycles and cliques) has chromatic...

Petersen graphs are regular graphs of degree three, so according to Brooks' theorem their chromatic number can only be two or three. More exactly: χ (...

In mathematics, the Fourier inversion theorem says that for many types of functions it is possible to recover a function from its Fourier transform. Intuitively...

which has 11 vertices but has maximum degree 5 and is not regular. By Brooks’ theorem, every k {\displaystyle k} -regular graph (except for odd cycles and...

Rowland Leonard Brooks (February 6, 1916 – June 18, 1993) was an English mathematician, known for proving Brooks's theorem on the relation between the...

adjacent vertices. It has been conjectured (combining Vizing's theorem and Brooks' theorem) that any graph has a total coloring in which the number of colors...

Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law...

In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D (surface in R...

partitioned. It equals the chromatic number of the square of the line graph. Brooks' theorem, applied to the square of the line graph, shows that the strong chromatic...

odd-length cycle graphs (the graphs that form the exceptional cases to Brooks' theorem) as well as the complete bipartite graphs and complete multipartite...

generalized Stokes theorem (sometimes with apostrophe as Stokes' theorem or Stokes's theorem), also called the Stokes–Cartan theorem, is a statement about...