mathematics, the Cauchy integral theorem (also known as the Cauchy–Goursat theorem) in complex analysis, named after Augustin-Louis Cauchy (and Édouard Goursat)...
10 KB (1,643 words) - 15:23, 27 May 2025
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a...
25 KB (4,364 words) - 04:10, 17 May 2025
compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. The residue theorem should not...
13 KB (3,290 words) - 09:31, 29 January 2025
Several theorems are named after Augustin-Louis Cauchy. Cauchy theorem may mean: Cauchy's integral theorem in complex analysis, also Cauchy's integral formula...
692 bytes (106 words) - 06:08, 19 November 2024
g. if the domain is simply connected; this is Cauchy's integral theorem, stating that the line integral of a holomorphic function along a closed curve...
9 KB (1,404 words) - 20:23, 21 May 2025
a first course in the subject: Cauchy's integral formula, Cauchy's integral theorem and estimates of complex integrals. Here is a brief sketch of this...
66 KB (9,149 words) - 10:47, 6 July 2025
t=0} . Cauchy's mean value theorem can be used to prove L'Hôpital's rule. The mean value theorem is the special case of Cauchy's mean value theorem when...
28 KB (5,401 words) - 07:03, 18 July 2025
who published most of Cauchy's works. They had two daughters, Marie Françoise Alicia (1819) and Marie Mathilde (1823). Cauchy's father was a highly ranked...
42 KB (5,401 words) - 03:26, 30 June 2025
In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D (surface in R...
23 KB (4,079 words) - 14:46, 30 June 2025
Contour integration (redirect from Contour integral)
of Cauchy's integral theorem The integral is reduced to only an integration around a small circle about each pole. application of the Cauchy integral formula...
47 KB (9,989 words) - 18:42, 12 July 2025
\end{aligned}}} By Cauchy's theorem, the left-hand integral is zero when f ( z ) {\displaystyle f(z)} is analytic (satisfying the Cauchy–Riemann equations)...
21 KB (3,183 words) - 03:16, 18 March 2025
Argument principle (redirect from Cauchy's argument principle)
In complex analysis, the argument principle (or Cauchy's argument principle) is a theorem relating the difference between the number of zeros and poles...
9 KB (1,612 words) - 07:49, 26 May 2025
theorem relates a contour integral around some of a function's poles to the sum of their residues Cauchy's integral formula Cauchy's integral theorem...
15 KB (3,101 words) - 12:03, 13 December 2024
mathematics, the Cauchy–Kovalevskaya theorem (also written as the Cauchy–Kowalevski theorem) is the main local existence and uniqueness theorem for analytic...
7 KB (986 words) - 03:07, 20 April 2025
boundary (as shown in Cauchy's integral formula). Path integrals in the complex plane are often used to determine complicated real integrals, and here the theory...
18 KB (2,538 words) - 09:09, 12 May 2025
closing a contour in the complex plane and applying Cauchy's integral theorem. The Fresnel integrals admit the following Maclaurin series that converge...
22 KB (2,714 words) - 16:58, 19 July 2025
f(x+iy)=u(x,y)+i\,v(x,y)} is holomorphic. Cauchy's integral theorem implies that the contour integral of every holomorphic function along a loop vanishes:...
25 KB (3,490 words) - 21:26, 15 June 2025
In complex analysis, Liouville's theorem, named after Joseph Liouville (although the theorem was first proven by Cauchy in 1844), states that every bounded...
14 KB (2,330 words) - 21:13, 31 March 2025
Fourier transform (redirect from Fourier integral)
by Cauchy's integral theorem. Therefore, the Fourier inversion formula can use integration along different lines, parallel to the real axis. Theorem: If...
177 KB (21,313 words) - 19:14, 8 July 2025
Uniformly Cauchy sequence Maclaurin–Cauchy test Cauchy's argument principle Cauchy inequality Cauchy's integral formula Cauchy's integral theorem Cauchy–Riemann...
3 KB (205 words) - 10:51, 15 May 2025
mathematics, the Cauchy principal value, named after Augustin-Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise...
11 KB (1,966 words) - 02:32, 14 June 2025
residues when one applies Cauchy's residue theorem. Rouché's theorem can also be used to give a short proof of the fundamental theorem of algebra. Let p ( z...
11 KB (1,885 words) - 11:53, 5 July 2025
(These two observations combine as real and imaginary parts in Cauchy's integral theorem.) In fluid dynamics, such a vector field is a potential flow....
34 KB (5,011 words) - 18:33, 3 July 2025
of the theorem, the first fundamental theorem of calculus, states that for a continuous function f , an antiderivative or indefinite integral F can be...
31 KB (4,883 words) - 05:40, 13 July 2025
in the volume enclosed. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called...
45 KB (7,538 words) - 18:50, 5 July 2025
common situation (for example, in the proof of Cauchy's repeated integration formula), the Leibniz integral rule becomes: d d x ( ∫ a x f ( x , t ) d t )...
53 KB (11,253 words) - 03:22, 22 June 2025
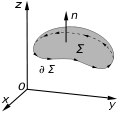
theorem, is a theorem in vector calculus on R 3 {\displaystyle \mathbb {R} ^{3}} . Given a vector field, the theorem relates the integral of the curl of...
30 KB (4,860 words) - 18:59, 5 July 2025
x_{n}^{0})} . Mathematics portal Cauchy boundary condition Cauchy horizon Hadamard, Jacques (1923). Lectures on Cauchy's Problem in Linear Partial Differential...
4 KB (637 words) - 22:54, 23 April 2025
as Picard's existence theorem, the Cauchy–Lipschitz theorem, or the existence and uniqueness theorem. The theorem is named after Émile Picard, Ernst Lindelöf...
21 KB (3,801 words) - 12:50, 10 July 2025
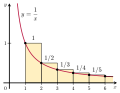
In mathematics, the integral test for convergence is a method used to test infinite series of monotonic terms for convergence. It was developed by Colin...
10 KB (1,727 words) - 01:02, 15 November 2024