Dattatreya Ramchandra Kaprekar (Marathi: दत्तात्रेय रामचंद्र कापरेकर; 17 January 1905 – 1986) was an Indian recreational mathematician who described several...

In number theory, Kaprekar's routine is an iterative algorithm named after its inventor, Indian mathematician D. R. Kaprekar. Each iteration starts with...

example, in base 10, 45 is a 2-Kaprekar number, because 45² = 2025, and 20 + 25 = 45. The numbers are named after D. R. Kaprekar. Let n {\displaystyle n} be...

The number 6174 is known as Kaprekar's constant after the Indian mathematician D. R. Kaprekar. This number is renowned for the following rule: Take any...

These numbers were first described in 1949 by the Indian mathematician D. R. Kaprekar. Let n {\displaystyle n} be a natural number. We define the b {\displaystyle...

Edwin Hubble Josephson constant – Brian David Josephson Kaprekar's constant – D. R. Kaprekar Kerr constant – John Kerr Khinchin's constant – Aleksandr...

as n-harshad (or n-Niven) numbers. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "harshad" comes from the Sanskrit...

Science, 1300-1800. Ákos Császár discovers the Császár polyhedron. D. R. Kaprekar discovers the convergence property of the number 6174. The use of lithium...

Gunjikar, K. R.; Kaprekar, D. R. (1939), "Theory of Demlo numbers" (PDF), Journal of the University of Bombay, VIII (3): 3–9 Kaprekar, D. R. (1938a), "On...

Hungarian dermatologist – Kaposi's sarcoma D. R. Kaprekar, Indian mathematician – Kaprekar constant, Kaprekar number Jacobus Kapteyn, Dutch astronomer –...

amateur mathematicians: List of recreational number theory topics Kulkarni, D. Enjoying Math: Learning Problem Solving With KenKen Puzzles Archived 2013-08-01...

these cubes as nasik as a respect to the great Indian Mathematician D R Kaprekar who hails from Deolali in Nasik District in Maharashtra, India. In 1905...

politician and sports administrator D. R. Kaprekar (1905–1986) — mathematician, discovered Kaprekar's constant and the Kaprekar number Sonali Kulkarni (born...

Rochester who works in Number Theory D. R. Kaprekar – Mathematician who worked on Number Theory. He is known for Kaprekar constant Narendra Karmarkar – Mathematician...

the People's Republic of China. The Malta Labour Party is founded. D. R. Kaprekar discovers the convergence property of the number 6174. Slavery in Kuwait...

Artillery (d. 1981) January 17 D. R. Kaprekar, Indian recreational mathematician (d. 1986) Saeb Salam, 4-time prime minister of Lebanon (d. 2000) Guillermo...

Bapudeva Sastri Damodar Dharmananda Kosambi Chandrashekhar Khare D. R. Kaprekar Dinesh Thakur Kapil Hari Paranjape M. N. Vartak Narendra Karmarkar Rahul...

considered by Damodar Dharmananda Kosambi. Kaprekar Constants: Numbers 495 and 6174. The Indian mathematician D.R.Kaprekar discovered the number 6174 is reached...

of Jesuits. Born: D. R. Kaprekar, Indian recreational mathematician; in Dahanu, Bombay province, British India (d. 1986) "Kaprekar numbers", where the...

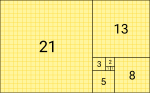
connected components. country calling code for Uzbekistan 999 = 33 × 37, Kaprekar number, Harshad number In some parts of the world, such as the UK and Commonwealth...

these numbers satisfy S d ( n , k ) = S ( n − d + 1 , k − d + 1 ) , n ≥ k ≥ d {\displaystyle S^{d}(n,k)=S(n-d+1,k-d+1),n\geq k\geq d} (hence the name "reduced")...

generalization: F n 2 − F n + r F n − r = ( − 1 ) n − r F r 2 {\displaystyle {F_{n}}^{2}-F_{n+r}F_{n-r}=(-1)^{n-r}{F_{r}}^{2}} F m F n + 1 − F m + 1 F...

Boston: Allyn and Bacon, LCCN 68-15225 Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766...

the original (PDF) on 2016-05-09, retrieved 2009-03-02. Bloch, R. M.; Campbell, R. V. D.; Ellis, M. (1948), "The Logical Design of the Raytheon Computer"...

{\displaystyle f(x,y)=x^{y}} defined on D = { ( x , y ) ∈ R 2 : x > 0 } {\displaystyle D=\{(x,y)\in \mathbf {R} ^{2}:x>0\}} . Then D can be viewed as a subset of...

+(a+dn-d)^{3}} is given by F ( d , a , n ) = ( n / 4 ) ( 2 a − d + d n ) ( 2 a 2 − 2 a d + 2 a d n − d 2 n + d 2 n 2 ) {\displaystyle F(d,a,n)=(n/4)(2a-d...

numbers q and r such that a = b q + r  and  r < b . {\displaystyle a=bq+r{\text{ and }}r<b.} The number q is called the quotient and r is called the remainder...

k > 1 we have d ( n ) n ε ≥ d ( k ) k ε {\displaystyle {\frac {d(n)}{n^{\varepsilon }}}\geq {\frac {d(k)}{k^{\varepsilon }}}} where d(n), the divisor...

root Sum-product Coding-related Meertens Other Dudeney Factorion Kaprekar Kaprekar's constant Keith Lychrel Narcissistic Perfect digit-to-digit invariant...

d d x e 1 x = − 1 x 2 ⋅ e 1 x {\displaystyle {\frac {\textrm {d}}{{\textrm {d}}x}}e^{\frac {1}{x}}=-{\frac {1}{x^{2}}}\cdot e^{\frac {1}{x}}} d 2 d x...