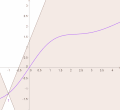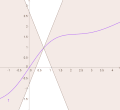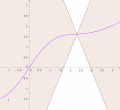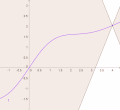
continuous function; there exist functions that are differentiable but not continuously differentiable (an example is given in the section Differentiability classes)...

differentiable functions. If a complex function is differentiable just once on an open set, it is both infinitely differentiable and analytic on that set [citation...

that the value of the right sub-function is used in this position. For a piecewise-defined function to be differentiable on a given interval in its domain...

mathematics, smooth functions (also called infinitely differentiable functions) and analytic functions are two very important types of functions. One can easily...

Weierstrass function, named after its discoverer, Karl Weierstrass, is an example of a real-valued function that is continuous everywhere but differentiable nowhere...

versions of the inverse function theorem for holomorphic functions, for differentiable maps between manifolds, for differentiable functions between Banach spaces...

and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally...

that interval. If a function is differentiable and convex then it is also continuously differentiable. A differentiable function of one variable is convex...

mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each...

Allendoerfer, Carl B. (1974). "Theorems about Differentiable Functions". Calculus of Several Variables and Differentiable Manifolds. New York: Macmillan. pp. 54–88...

another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold...

an implicit function that is differentiable in some small enough neighbourhood of (a, b); in other words, there is a differentiable function f that is defined...

to 1. Lipschitz continuous functions that are everywhere differentiable but not continuously differentiable The function f ( x ) = { x 2 sin ⁡ ( 1 /...

The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change...

theorem or Rolle's lemma essentially states that any real-valued differentiable function that attains equal values at two distinct points must have at least...

zero (note that this indicator function is not left differentiable at zero). If a real-valued, differentiable function f, defined on an interval I of...

derivatives are the result of differentiating a function repeatedly. Given that f {\displaystyle f} is a differentiable function, the derivative of f {\displaystyle...

properties: V is differentiable everywhere The derivative V ′ is bounded everywhere The derivative is not Riemann-integrable. The function is defined by...

In mathematics, the Fabius function is an example of an infinitely differentiable function that is nowhere analytic, found by Jaap Fabius (1966). It was...

and differentiable functions f and g, d ( a f + b g ) = a d f + b d g . {\displaystyle d(af+bg)=a\,df+b\,dg.} Product rule: For two differentiable functions...

calculus, the inverse function rule is a formula that expresses the derivative of the inverse of a bijective and differentiable function f in terms of the...

Weierstrass function, a function that is continuous everywhere but differentiable nowhere. The sum of a differentiable function and the Weierstrass function is...

a\}} are convex sets. A differentiable function f is (strictly) concave on an interval if and only if its derivative function f ′ is (strictly) monotonically...

of a scalar-valued differentiable function f {\displaystyle f} of several variables is the vector field (or vector-valued function) ∇ f {\displaystyle...

mechanical and electrical engineering. As a differentiable function of a complex variable is equal to the sum function given by its Taylor series (that is, it...

two differentiable functions f and g in terms of the derivatives of f and g. More precisely, if h = f ∘ g {\displaystyle h=f\circ g} is the function such...

be differentiable for its Jacobian matrix to be defined, since only its first-order partial derivatives are required to exist. If f is differentiable at...

Taylor's theorem gives an approximation of a k {\textstyle k} -times differentiable function around a given point by a polynomial of degree k {\textstyle k}...

{d^{k}}{dx^{k}}}g(x)} Differentiable function – Mathematical function whose derivative exists Differential of a function – Notion in calculus Differentiation of integrals –...

In vector calculus, an invex function is a differentiable function f {\displaystyle f} from R n {\displaystyle \mathbb {R} ^{n}} to R {\displaystyle \mathbb...