In Euclidean geometry, a plane is a flat two-dimensional surface that extends indefinitely. Euclidean planes often arise as subspaces of three-dimensional...

the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces...

the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are...

In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted E 2 {\displaystyle {\textbf {E}}^{2}} or E 2 {\displaystyle \mathbb {E}...

two coordinates or they can move in two independent directions. Common two-dimensional spaces are often called planes, or, more generally, surfaces. These...

In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is...

Four-dimensional space (4D) is the mathematical extension of the concept of three-dimensional space (3D). Three-dimensional space is the simplest possible...

is six-dimensional Euclidean space, in which 6-polytopes and the 5-sphere are constructed. Six-dimensional elliptical space and hyperbolic spaces are also...

indefinitely extended in a two-dimensional plane that are both perpendicular to a third line (in the same plane): In Euclidean geometry, the lines remain...

in the Euclidean plane The distance from a point to a plane in three-dimensional Euclidean space The distance between two lines in three-dimensional Euclidean...

the physical world. However, the three-dimensional "space part" of the Minkowski space remains the space of Euclidean geometry. This is not the case with...

dimension) and three-dimensional space. When working exclusively in two-dimensional Euclidean space, the definite article is used, so the Euclidean plane...

In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space E n {\displaystyle \mathbb {E} ^{n}} ; that is, the transformations...

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent...

A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because...

be cell-transitive or isochoric. In the 3-dimensional euclidean space, a cell of such a honeycomb is said to be a space-filling polyhedron. A necessary...

a Euclidean space of dimension n, En (Euclidean line, E; Euclidean plane, E2; Euclidean three-dimensional space, E3) form a real coordinate space of...

projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way...

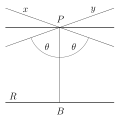
geometry. The parallel postulate of Euclidean geometry is replaced with: For any given line R and point P not on R, in the plane containing both line R and point...

In mathematics, a zero-dimensional topological space (or nildimensional space) is a topological space that has dimension zero with respect to one of several...

that exist in five-dimensional space. Four-dimensional space — a foundational step to understanding five-dimensional extensions. 5D Euclidean geometry designated...

interval in spacetime between events. Minkowski space differs from four-dimensional Euclidean space insofar as it treats time differently from the three spatial...

one-dimensional space, regardless of the dimension of the ambient space in which the line or curve is embedded. Examples include the circle on a plane, or...

"elliptic space" to refer specifically to 3-dimensional elliptic geometry. This is in contrast to the previous section, which was about 2-dimensional elliptic...

the points of a three-dimensional Euclidean space are uniquely determined by Euclid's axioms, and all three-dimensional Euclidean spaces are considered...

called 7-dimensional space. Often such a space is studied as a vector space, without any notion of distance. Seven-dimensional Euclidean space is seven-dimensional...

In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible...

the geometry of three-dimensional Euclidean space (3D space). A solid figure is the region of 3D space bounded by a two-dimensional closed surface; for...

called 8-dimensional space. Often such spaces are studied as vector spaces, without any notion of distance. Eight-dimensional Euclidean space is eight-dimensional...

Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions...