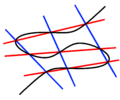
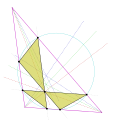
projective geometry, five points determine a conic (a degree-2 plane curve), just as two (distinct) points determine a line (a degree-1 plane curve)...
15 KB (2,331 words) - 02:28, 23 September 2023
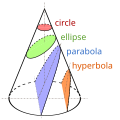
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola...
69 KB (9,174 words) - 17:05, 5 June 2025
linear position (no three on a line), there is a pencil of conics through them (five points determine a conic, four points leave one parameter free), of...
16 KB (2,645 words) - 13:58, 5 June 2025
York City Five points determine a conic Five Points Correctional Facility, Romulus, New York Five Points of Calvinism Le Corbusier's Five Points of Architecture...
3 KB (358 words) - 19:47, 10 April 2025
that points should impose independent conditions on curves passing through them. For example, five points determine a conic, but in general six points do...
10 KB (1,469 words) - 21:00, 5 March 2025
points are allowed to be collinear, and six points are allowed to lie on a conic (in general two points determine a line and five points determine a conic)...
11 KB (1,492 words) - 19:47, 3 May 2025
Cramer's theorem (algebraic curves) (redirect from Three points determine a circle)
a line (of degree 1) is determined by 2 distinct points on it: one and only one line goes through those two points. Likewise, a non-degenerate conic (polynomial...
6 KB (1,088 words) - 19:32, 3 May 2025
to two points determining a line and how five points determine a conic. If two cubics pass through a given set of nine points, then in fact a pencil of...
20 KB (2,876 words) - 13:32, 4 July 2025
Pascal's theorem (category Conic sections)
points on a conic about which special statements can be made, as five points determine a conic. The converse is the Braikenridge–Maclaurin theorem, named for...
17 KB (2,198 words) - 00:12, 23 June 2024
coordinates, and five points determine a conic, if the points are in general linear position, as passing through a given point imposes a linear condition...
9 KB (1,137 words) - 20:03, 11 March 2025
Cross-ratio (category Pages that use a deprecated format of the math tags)
points determine a conic, but six general points do not lie on a conic, so whether any 6-tuple of points lies on a conic is also a projective invariant...
30 KB (4,844 words) - 22:03, 13 May 2025
} In geometry, five points determine a conic, so arbitrary sets of six points do not generally lie on a conic section, let alone a circle. Nevertheless...
3 KB (498 words) - 03:14, 5 July 2025
Pencil (geometry) (redirect from Pencil of conics)
field any two conics meet in four points (counted with multiplicity) and so, determine the pencil of conics based on these four points. Furthermore, the...
20 KB (2,937 words) - 19:33, 17 June 2025
Sphere (redirect from Volume of a sphere)
great-circle distances from a pair of foci is a constant Many theorems relating to planar conic sections also extend to spherical conics. If a sphere is intersected...
41 KB (5,342 words) - 15:01, 12 May 2025
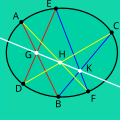
discovered this result. This hyperbola is the unique conic which passes through the five points A, B, C, G, O. The three triangles △XBC, △YCA, △ZAB erected...
14 KB (1,597 words) - 15:30, 1 July 2025
Y\}.} Given a conic C and a point P not on it, two distinct secant lines through P intersect C in four points. These four points determine a quadrangle...
38 KB (5,099 words) - 22:20, 24 May 2025
Analytic geometry (redirect from Equation of a curve)
zeros, one can consider conics as points in the five-dimensional projective space P 5 . {\displaystyle \mathbf {P} ^{5}.} The conic sections described by...
40 KB (5,612 words) - 13:05, 2 June 2025
parallel, then the surface of revolution is a circular cylinder. In analogy with the conic sections, the set of points whose Cartesian coordinates satisfy the...
34 KB (4,825 words) - 21:40, 24 June 2025
Straightedge and compass construction (section Constructing a triangle from three given characteristic points or lengths)
axioms can construct exactly the same set of points as the extended constructions using a compass and conic drawing tool. Therefore, origami can also be...
36 KB (4,826 words) - 07:34, 9 June 2025
Bézout's theorem. However, five points are needed to define a nondegenerate conic, so again in this case there is no paradox. In a letter to Euler, Cramer...
7 KB (955 words) - 10:21, 6 December 2024
orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections...
27 KB (2,869 words) - 06:33, 5 July 2025
diametrically opposite points, called antipodal points. Any two points that are not antipodal points determine a unique great circle. There is a natural unit of...
15 KB (1,955 words) - 04:41, 4 July 2025
Every quadratic equation in X, Y, and Z determines a unique conic, its vanishing locus. Conversely, every conic in the complex projective plane has an...
99 KB (12,273 words) - 21:30, 5 July 2025
Discriminant (redirect from Discriminant of a polynomial)
a c , {\displaystyle b^{2}-ac,} and determines the shape of the conic section. If this discriminant is negative, the curve either has no real points,...
41 KB (6,704 words) - 20:17, 23 June 2025
all conics are defined as the solution set of an equation of a plane and of the equation of a cone just given. This formalism allows one to determine the...
32 KB (4,249 words) - 19:03, 26 March 2025
aimed at both practical goals (e.g., establishing a reliable calendar or determining how to cure a variety of illnesses) as well as more abstract investigations...
52 KB (6,342 words) - 23:56, 22 May 2025
Poncelet–Steiner theorem (section Points at Infinity)
of points on the arc of a circle. Similarly, though there is no specialized term for it, five points in the plane define a conic section, any five points...
94 KB (13,156 words) - 20:50, 25 June 2025
Longitude (redirect from Length of a degree of longitude)
response to the problems of navigation, a number of European maritime powers offered prizes for a method to determine longitude at sea. The best-known of...
38 KB (4,438 words) - 04:02, 11 June 2025
Quadratic equation (redirect from Factoring a quadratic expression)
{\displaystyle x^{2}-x-1=0.} The equations of the circle and the other conic sections—ellipses, parabolas, and hyperbolas—are quadratic equations in...
53 KB (6,663 words) - 16:21, 26 June 2025