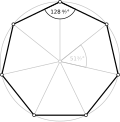
In algebraic geometry, the function field of an algebraic variety V consists of objects that are interpreted as rational functions on V. In classical...

of an algebraic function field is not a well-defined notion. The algebraic function fields over k form a category; the morphisms from function field K...

Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as...

used in algebraic geometry. There the function field of an algebraic variety V is formed as the field of fractions of the coordinate ring of V (more accurately...

In algebraic geometry, a morphism between algebraic varieties is a function between the varieties that is given locally by polynomials. It is also called...

specifically in algebraic geometry, the dimension of an algebraic variety may be defined in various equivalent ways. Some of these definitions are of geometric...

The sheaf of rational functions KX of a scheme X is the generalization to scheme theory of the notion of function field of an algebraic variety in classical...

fields: Algebraic number field: A finite extension of Q {\displaystyle \mathbb {Q} } Global function field: The function field of an irreducible algebraic curve...

mathematics, an algebraic structure or algebraic system consists of a nonempty set A (called the underlying set, carrier set or domain), a collection of operations...

projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by...

real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics. The...

Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometrical problems...

In the mathematical field of algebraic geometry, a singular point of an algebraic variety V is a point P that is 'special' (so, singular), in the geometric...

Function field may refer to: Function field of an algebraic variety Function field (scheme theory) Algebraic function field Function field sieve Function...

Spaltenstein variety Arithmetic genus, geometric genus, irregularity Tangent space, Zariski tangent space Function field of an algebraic variety Ample line...

in algebraic geometry, complex analysis and algebraic number theory, an abelian variety is a smooth projective algebraic variety that is also an algebraic...

In algebraic geometry, an affine algebraic set is the set of the common zeros over an algebraically closed field k of some family of polynomials in the...

universal algebra, a variety of algebras or equational class is the class of all algebraic structures of a given signature satisfying a given set of identities...

mathematics, a rational variety is an algebraic variety, over a given field K, which is birationally equivalent to a projective space of some dimension over...

algebra, an adelic algebraic group is a semitopological group defined by an algebraic group G over a number field K, and the adele ring A = A(K) of K...

specifically algebraic geometry, a scheme is a structure that enlarges the notion of algebraic variety in several ways, such as taking account of multiplicities...

the Hasse–Weil zeta function attached to an algebraic variety V defined over an algebraic number field K is a meromorphic function on the complex plane...

In algebraic geometry, divisors are a generalization of codimension-1 subvarieties of algebraic varieties. Two different generalizations are in common...

projective algebraic variety over the field Fq with q elements and Nk is the number of points of V defined over the finite field extension Fqk of Fq. Making...

sense of functions defined on algebraic varieties or manifolds, or of algebraic number fields examined at a particular place, or prime. Local algebra is...

used for the study of algebraic varieties, which are solution sets of systems of polynomial equations. Weyl algebras and Lie algebras may be considered...

In field theory, a branch of algebra, an algebraic field extension E / F {\displaystyle E/F} is called a separable extension if for every α ∈ E {\displaystyle...

Diophantine equations and are typically functions from a set of points on algebraic varieties (or a set of algebraic varieties) to the real numbers. For instance...

function defined on M. More generally, given an algebraic variety V over some field K, the function field K(V), consisting of the rational functions defined...

in terms of properties of algebraic objects such as algebraic number fields and their rings of integers, finite fields, and function fields. These properties...