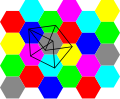
More unsolved problems in mathematics In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the...

are necessary to contain the original Hadwiger's conjecture on dissection into orthoschemes Hadwiger–Nelson problem on the chromatic number of unit distance...

contributed to the study of the Hadwiger–Nelson problem in geometric graph theory, making the first progress on the problem in over 60 years. De Grey is...

with a forbidden induced tree The Hadwiger conjecture relating coloring to clique minors The Hadwiger–Nelson problem on the chromatic number of unit distance...

from the utility graph K3,3 by subdividing one of its edges. The Hadwiger–Nelson problem asks how many colors are needed to color the points of the Euclidean...

problem, also now known as the Hadwiger–Nelson problem, was a favorite of Paul Erdős, who mentioned it frequently in his problems lectures. In 2018, Aubrey...

proven in the plane, but remains open in higher dimensions. The Hadwiger–Nelson problem concerns the minimum number of colors needed to color the points...

Grötzsch's theorem: triangle-free planar graphs are 3-colorable. Hadwiger–Nelson problem: how many colors are needed to color the plane so that no two points...

sets to infinite ones, and reducing the Hadwiger–Nelson problem on the chromatic number of the plane to a problem about finite graphs. It may be generalized...

like the simpler Moser spindle, it provides a lower bound for the Hadwiger–Nelson problem: coloring the points of the Euclidean plane so that each unit line...

Logarithm Problem, by René Schoof Hadwiger’s Conjecture, by Paul Seymour The Hadwiger–Nelson Problem, by Alexander Soifer Erdős’s Unit Distance Problem, by...

colors required to color unit distance graphs is also unknown (the Hadwiger–Nelson problem): some unit distance graphs require five colors, and every unit...

pairs of points that are a unit distance apart in the plane. The Hadwiger–Nelson problem concerns the chromatic number of these graphs. An intersection...

square grid is 15, by Subercaseaux and Heule in 2023 (See also: Hadwiger–Nelson problem for the chromatic number of the plane) Formal verification – Proving...

development of these areas, concentrating in particular on the Hadwiger–Nelson problem and on the biography of Bartel Leendert van der Waerden. It was...

but is not an isometry. To do so, following known results on the Hadwiger–Nelson problem, color the points of the given space with a finite number of colors...

graph theory, Isbell was the first to prove the bound χ ≤ 7 on the Hadwiger–Nelson problem, the question of how many colors are needed to color the points...

open problems in graph theory and combinatorics. As well as her thesis work on matroids, she has also published research on the Hadwiger–Nelson problem concerning...

the Rural Midwest, 1945-1985." Old Northwest 16 (1992): 13-36. Don F. Hadwiger, and Clay Cochran, "Rural telephones in the United States." Agricultural...