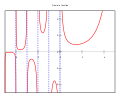
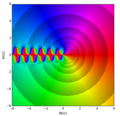
In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables s with Re(s) > 1 and a ≠ 0,...
22 KB (4,220 words) - 10:29, 14 August 2024
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined...
71 KB (10,620 words) - 17:42, 9 December 2024
zeta function of a variety Height zeta function of a variety Hurwitz zeta function, a generalization of the Riemann zeta function Igusa zeta function...
3 KB (379 words) - 14:35, 7 September 2023
Lerch transcendent (redirect from Hurwitz-Lerch zeta function)
mathematics, the Lerch transcendent, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after Czech mathematician...
17 KB (3,658 words) - 00:56, 15 October 2024
(z)=\zeta _{H}'(0,z)-\zeta '(0),} where ζ H {\displaystyle \zeta _{H}} is the Hurwitz zeta function, ζ {\displaystyle \zeta } is the Riemann zeta function...
91 KB (13,517 words) - 14:35, 30 October 2024
t\\&=(-1)^{m+1}m!\zeta (m+1,z)\end{aligned}}} where ζ ( s , q ) {\displaystyle \zeta (s,q)} is the Hurwitz zeta function. This expresses the polygamma function as the...
12 KB (2,364 words) - 04:32, 14 September 2024
Polylogarithm (redirect from De Jonquière's function)
polylogarithm function is equivalent to the Hurwitz zeta function — either function can be expressed in terms of the other — and both functions are special...
60 KB (10,165 words) - 14:52, 17 June 2024
} making it a special case of the Hurwitz zeta function ψ 1 ( z ) = ζ ( 2 , z ) . {\displaystyle \psi _{1}(z)=\zeta (2,z).} Note that the last two formulas...
6 KB (1,125 words) - 12:09, 15 December 2024
Multiplication theorem (redirect from Periodic zeta function)
periodic zeta function occurs in the reflection formula for the Hurwitz zeta function, which is why the relation that it obeys, and the Hurwitz zeta relation...
10 KB (1,969 words) - 21:07, 9 November 2023
L-functions may be written as a linear combination of the Hurwitz zeta function at rational values. Fixing an integer k ≥ 1, the Dirichlet L-functions for...
11 KB (1,701 words) - 16:44, 23 December 2024
coefficients of higher order with Gn(1) = Gn, Γ is the gamma function and ζ is the Hurwitz zeta function. Similar series with the Cauchy numbers of the second...
35 KB (7,102 words) - 11:53, 15 December 2024
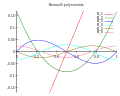
Bernoulli polynomials (redirect from Bernoulli function)
special functions and, in particular, the Riemann zeta function and the Hurwitz zeta function. They are an Appell sequence (i.e. a Sheffer sequence for...
19 KB (4,328 words) - 10:06, 30 November 2024
first studied by Takuro Shintani (1976). They include Hurwitz zeta functions and Barnes zeta functions. Let P ( x ) {\displaystyle P(\mathbf {x} )} be a polynomial...
3 KB (481 words) - 17:57, 9 November 2020
} The Legendre chi function appears as the discrete Fourier transform, with respect to the order ν, of the Hurwitz zeta function, and also of the Euler...
2 KB (519 words) - 17:00, 14 December 2023
and the Riemann zeta function or the Hurwitz zeta function. Specifically, given a real number x, the rational zeta series for x is given by x = ∑ n = 2...
6 KB (1,434 words) - 16:12, 5 July 2024
Dirichlet beta function Dirichlet L-function Hurwitz zeta function Legendre chi function Lerch transcendent Polylogarithm and related functions: Incomplete...
10 KB (1,065 words) - 20:52, 29 October 2024
{1}{k}}-\log n-\sum _{m=2}^{\infty }{\frac {\zeta (m,n+1)}{m}}\right),} where ζ(s, k) is the Hurwitz zeta function. The sum in this equation involves the harmonic...
71 KB (9,540 words) - 19:50, 21 December 2024
{\displaystyle N} approaches infinity, this becomes the Hurwitz zeta function ζ ( s , q ) {\displaystyle \zeta (s,q)} . For finite N {\displaystyle N} and q =...
7 KB (684 words) - 22:37, 14 July 2024
quaternion Hurwitz scheme Hurwitz surface Hurwitz zeta function Hurwitz's automorphisms theorem Hurwitz's theorem (complex analysis) Hurwitz's theorem (composition...
9 KB (984 words) - 22:46, 5 November 2024
Re(s) > 0. Alternatively, the following definition, in terms of the Hurwitz zeta function, is valid in the whole complex s-plane: β ( s ) = 4 − s ( ζ ( s...
8 KB (1,420 words) - 13:32, 12 October 2024
The multiplication theorem for the Hurwitz zeta function ζ ( s , a ) = ∑ n = 0 ∞ ( n + a ) − s {\displaystyle \zeta (s,a)=\sum _{n=0}^{\infty }(n+a)^{-s}}...
7 KB (1,222 words) - 02:36, 4 May 2024
{\bigl [}\zeta '(-1,z)-\zeta '(-1){\bigr ]}} where ζ′(z) denotes the derivative of the Riemann zeta function, ζ(a,z) denotes the Hurwitz zeta function and ζ...
5 KB (919 words) - 14:41, 21 October 2024
{\displaystyle H_{n,m}=\zeta (m,1)-\zeta (m,n+1),} where ζ ( m , n ) {\displaystyle \zeta (m,n)} is the Hurwitz zeta function. This relationship is used...
40 KB (5,537 words) - 18:05, 17 October 2024
tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function. The Clausen function of order 2 – often referred...
31 KB (6,497 words) - 04:56, 5 December 2024
Functional determinant (section Zeta function version)
{\displaystyle -\partial _{s}\zeta _{H}(0,a)} , where ζ H ( s , a ) {\displaystyle \zeta _{H}(s,a)} is the Hurwitz zeta function. We will compute the determinant...
15 KB (2,716 words) - 09:52, 12 November 2024
number Genocchi number Kummer's congruences Poly-Bernoulli number Hurwitz zeta function Euler summation Stirling polynomial Sums of powers Translation of...
93 KB (13,022 words) - 00:11, 17 December 2024
polynomials are given in terms of the Hurwitz zeta function: ζ ( s , a ) = ∑ n = 0 ∞ 1 ( n + a ) s {\displaystyle \zeta (s,a)=\sum _{n=0}^{\infty }{\frac...
27 KB (4,751 words) - 03:20, 21 December 2024
continuing ζ ( s ) {\displaystyle \zeta (s)} . Faulhaber's formula can be written in terms of the Hurwitz zeta function: ∑ k = 1 n k p = ζ ( − p ) − ζ (...
34 KB (8,032 words) - 08:16, 2 December 2024
\left(k+q\right)^{s}}}~.} [clarification needed] The constant C is the Hurwitz zeta function evaluated at s. Zipfian distributions can be obtained from Pareto...
47 KB (4,653 words) - 10:55, 22 December 2024
that paper, a slightly non-standard definition is used for the Hurwitz zeta function. Weisstein, Eric W. "Khinchin's constant". MathWorld. Ryll-Nardzewski...
11 KB (1,916 words) - 01:54, 10 December 2024