measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure...

graph of that function and the X axis. The Lebesgue integral, named after French mathematician Henri Lebesgue, is one way to make this concept rigorous...

In mathematics, the Lebesgue differentiation theorem is a theorem of real analysis, which states that for almost every point, the value of an integrable...

Vitali set is an elementary example of a set of real numbers that is not Lebesgue measurable, found by Giuseppe Vitali in 1905. The Vitali theorem is the...

In mathematical analysis, a null set is a Lebesgue measurable set of real numbers that has measure zero. This can be characterized as a set that can be...

limit emphasizes that any point mass located at 0 is entirely captured by the Laplace transform. Although with the Lebesgue integral, it is not necessary...

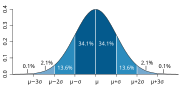
for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable X is often denoted...

distribution function FX of X, with the expected value of g(X) now given by the Lebesgue–Stieltjes integral E ⁡ [ g ( X ) ] = ∫ − ∞ ∞ g ( x ) d F X ( x ) . {\displaystyle...

of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue, Nikolai Luzin, Johann Radon, Constantin Carathéodory, and Maurice Fréchet...

This concept is important in mathematical analysis as the foundation for Lebesgue integration, and in probability theory, where it is interpreted as the...

definite integral of a step function is a piecewise linear function. The Lebesgue integral of a step function f = ∑ i = 0 n α i χ A i {\displaystyle \textstyle...

{\displaystyle f} is a Lebesgue measurable function on G ( Ω ) {\displaystyle G(\Omega )} , then f ∘ G {\displaystyle f\circ G} is Lebesgue measurable on Ω {\displaystyle...

{\displaystyle f:\mathbb {R} \to \mathbb {C} } is called (Lebesgue) integrable if the Lebesgue integral of its absolute value is finite: ‖ f ‖ 1 = ∫ R |...

continuous univariate case above, the reference measure is the Lebesgue measure. The probability mass function of a discrete random variable is the density with...

if f represented mass density and μ was the Lebesgue measure in three-dimensional space R3, then ν(A) would equal the total mass in a spatial region...

X {\displaystyle F_{X}} is absolutely continuous, then there exists a Lebesgue-integrable function f X ( x ) {\displaystyle f_{X}(x)} such that F X (...

construction which is similar to the construction by Robin Thomas of a non-Lebesgue measurable set with some additional properties appeared in American Mathematical...

by Stieltjes. It serves as an instructive and useful precursor of the Lebesgue integral, and an invaluable tool in unifying equivalent forms of statistical...

allowing only Lebesgue measurable pieces one obtains: If A and B are subsets of Rn with non-empty interiors, then they have equal Lebesgue measures if and...

converges to the expected value: (Lebesgue integrability of Xj means that the expected value E(Xj) exists according to Lebesgue integration and is finite. It...

function against this mass distribution. Formally, the Lebesgue integral provides the necessary analytic device. The Lebesgue integral with respect to...

Lebesgue integral of any such function would be zero. In general, distributions can be described as a discrete distribution (with a probability mass function)...

insignificant since initial conditions with zero angular momentum are rare, having Lebesgue measure zero. An important issue in proving this result is the fact that...

the length of the curve, and the two-dimensional Hausdorff measure of a Lebesgue-measurable subset of R 2 {\displaystyle \mathbb {R} ^{2}} is proportional...

mathematical model used in language processing and speech recognition Lebesgue measure, in measure theory Levenberg–Marquardt algorithm, used to solve...

almost everywhere. In dimension 1, and when μ {\displaystyle \mu } is the Lebesgue measure over the unit interval, the result specializes to Ryff's theorem...

{\displaystyle {\mathcal {F}}} is the σ-algebra of Borel sets on Ω, and P is the Lebesgue measure on [0,1]. In this case, the open intervals of the form (a,b), where...

R n {\displaystyle \mathbb {R} ^{n}} via the Lebesgue measure. In the one-dimensional case, the Lebesgue outer measure of a set is defined in terms of...

statistics to estimate a probability density function of a random variable Lebesgue's density theorem Schnirelmann density Natural density (also called asymptotic...

"point mass" at 0. {\displaystyle 0.} However, the Dirac measure δ 0 {\displaystyle \delta _{0}} is not absolutely continuous with respect to Lebesgue measure...