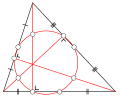
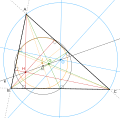
The orthocenter of a triangle, usually denoted by H, is the point where the three (possibly extended) altitudes intersect. The orthocenter lies inside...

three altitudes intersect in a single point, called the orthocenter of the triangle. The orthocenter lies inside the triangle if and only if the triangle...

orthocentric system is a set of four points on a plane, one of which is the orthocenter of the triangle formed by the other three. Equivalently, the lines passing...

triangle. The orthocenter of a triangle, usually denoted by H, is the point where the three (possibly extended) altitudes intersect. The orthocenter lies inside...

midpoint of the line segment from each vertex of the triangle to the orthocenter (where the three altitudes meet; these line segments lie on their respective...

several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the...

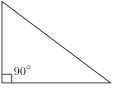
Since these intersect at the right-angled vertex, the right triangle's orthocenter—the intersection of its three altitudes—coincides with the right-angled...

orthic axis of △ABC. The isogonal conjugate of the circumcenter X3 is the orthocenter X4 (also denoted by H) having trilinear coordinates sec A : sec B : sec...

circle of the triangle. Together with the centroid, circumcenter, and orthocenter, it is one of the four triangle centers known to the ancient Greeks,...

between that triangle's orthocenter H and circumcenter O. The centroid G also lies on the same line, 2/3 of the way from the orthocenter to the circumcenter...

while the orthocenter and the circumcenter are in an acute triangle's interior, they are exterior to an obtuse triangle. The orthocenter is the intersection...

center and points such as a centroid. However, there is generally no orthocenter in the sense of intersecting altitudes. Gaspard Monge found a center...

concurrent. This common point is called the tetrahedron orthocenter (a generalization of the orthocenter of a triangle). It has the property that it is the...

mathematician Gaston Albert Gohierre de Longchamps. It is the reflection of the orthocenter of the triangle about the circumcenter. Let the given triangle have vertices...

states that the orthocenter of the diagonal triangle of a cyclic quadrilateral is the circumcenter of the cyclic quadrilateral. Orthocenter Power of a point...

the triangle. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions...

geometric theorem that the altitudes of a triangle always meet in a single orthocenter. Gauss was concerned with John Napier's "Pentagramma mirificum" – a certain...

the area of each is 1/4 the area of the original triangle.: p.177  The orthocenter of the medial triangle coincides with the circumcenter of triangle △ABC...

of a non-equilateral triangle is the circle that has the triangle's orthocenter and centroid at opposite ends of its diameter. This diameter also contains...

and orthocenter. The line that passes through all of them is known as the Euler line. The isogonal conjugate of the circumcenter is the orthocenter. The...

triangle is then △LMN. If △ABC is not an obtuse triangle and P is the orthocenter, then the angles of △LMN are 180° − 2A, 180° − 2B and 180° − 2C. The...

Neuberg cubic passes through the following points: incenter, circumcenter, orthocenter, both Fermat points, both isodynamic points, the Euler infinity point...

collineation. In any triangle the following sets of points are collinear: The orthocenter, the circumcenter, the centroid, the Exeter point, the de Longchamps...

yC, f) be the three corresponding vanishing points respectively. The orthocenter of the triangle with vertices in the three vanishing points is the intersection...

is continuous: Construct the orthocenter of triangle and three midpoints (say A', B' C' ) between vertices and orthocenter. Construct a circumcircle of...

polar circle of a triangle is the circle whose center is the triangle's orthocenter and whose squared radius is r 2 = H A ¯ × H D ¯ = H B ¯ × H E ¯ = H C...

intersection of the lines lies on the nine-point circle. Letting H denote the orthocenter of the triangle ABC, the Simson line of P bisects the segment PH in a...

concerns a property of two perpendicular lines intersecting at a triangle's orthocenter. Harcourt's theorem concerns the relationship of line segments through...

However, triangle centers such as the centroid, circumcenter, incenter and orthocenter are not invariant, because moving a triangle will also cause its centers...

incenter, the circumcenter, the nine-point center, the centroid and the orthocenter. In addition to the sides and diagonals of a quadrilateral, some important...