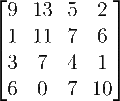In mathematics, a symmetric matrix M {\displaystyle \ M\ } with real entries is positive-definite if the real number x ⊤ M x {\displaystyle \...
50 KB (8,593 words) - 22:43, 3 January 2025
functional Positive-definite kernel Positive-definite matrix Positive-definite quadratic form Fasshauer, Gregory E. (2011), "Positive definite kernels:...
1 KB (147 words) - 17:53, 26 April 2021
branch of mathematics, a positive-definite kernel is a generalization of a positive-definite function or a positive-definite matrix. It was first introduced...
23 KB (4,246 words) - 04:02, 25 December 2024
that sign, the quadratic form is called positive-definite or negative-definite. A semidefinite (or semi-definite) quadratic form is defined in much the...
7 KB (1,202 words) - 18:41, 10 June 2022
positive semidefinite matrix A as BTB = A, as in the Cholesky factorization, even if BB ≠ A. This distinct meaning is discussed in Positive definite matrix...
29 KB (4,651 words) - 04:08, 1 January 2025
a_{ij}=f(x_{i}-x_{j})} is a positive semi-definite matrix.[citation needed] By definition, a positive semi-definite matrix, such as A {\displaystyle A}...
7 KB (1,175 words) - 07:16, 11 October 2024
Cholesky decomposition (category Matrix decompositions)
shə-LES-kee) is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful...
51 KB (7,649 words) - 09:52, 5 November 2024
Polar decomposition (redirect from Matrix polar decomposition)
is a positive semi-definite Hermitian matrix ( U {\displaystyle U} is an orthogonal matrix and P {\displaystyle P} is a positive semi-definite symmetric...
25 KB (4,218 words) - 12:36, 19 December 2024
M. A 2×2 matrix with two distinct nonzero eigenvalues has four square roots. A positive-definite matrix has precisely one positive-definite square root...
8 KB (1,360 words) - 01:35, 6 January 2025
eigenvalues). A symmetric totally positive matrix is therefore also positive-definite. A totally non-negative matrix is defined similarly, except that...
3 KB (379 words) - 19:18, 13 January 2024
Schur product theorem (category Matrix theory)
theorem states that the Hadamard product of two positive definite matrices is also a positive definite matrix. The result is named after Issai Schur (Schur...
7 KB (1,661 words) - 19:09, 23 November 2024
determinant is a polynomial of degree 3. The Hessian matrix of a convex function is positive semi-definite. Refining this property allows us to test whether...
22 KB (3,537 words) - 17:18, 22 December 2024
triangular with real positive diagonal entries Comment: if the matrix A {\displaystyle A} is Hermitian and positive semi-definite, then it has a decomposition...
26 KB (3,580 words) - 17:05, 12 March 2024
The stiffness matrix is symmetric, i.e. Aij = Aji, so all its eigenvalues are real. Moreover, it is a strictly positive-definite matrix, so that the system...
8 KB (1,264 words) - 09:11, 4 December 2024
exists a positive definite symmetric matrix W such that W − GTWG is positive definite. Semipositivity and diagonal dominance A is semi-positive. That is...
9 KB (1,174 words) - 22:53, 5 November 2024
real non-singular matrix can be uniquely factored as the product of an orthogonal matrix and a symmetric positive definite matrix, which is called a...
17 KB (2,812 words) - 00:30, 16 December 2024
the symmetric positive-definite matrix Σ = [ A B B T C ] , {\displaystyle \Sigma =\left[{\begin{matrix}A&B\\B^{\mathrm {T} }&C\end{matrix}}\right],} where...
15 KB (2,901 words) - 13:16, 1 July 2024
apparent. If A and B are both symmetric or Hermitian, and B is also a positive-definite matrix, the eigenvalues λi are real and eigenvectors v1 and v2 with distinct...
40 KB (5,590 words) - 15:14, 28 October 2024
{\displaystyle U} is a p × p {\displaystyle p\times p} positive definite matrix with a matrix variate beta distribution, and a , b > ( p − 1 ) / 2 {\displaystyle...
5 KB (1,005 words) - 22:59, 18 December 2024
neither positive-semidefinite nor negative-semidefinite. A symmetric matrix is positive-definite if and only if all its eigenvalues are positive. The table...
16 KB (1,831 words) - 00:24, 24 September 2024
neither positive-semidefinite nor negative-semidefinite. A symmetric matrix is positive-definite if and only if all its eigenvalues are positive, that is...
108 KB (13,476 words) - 20:11, 11 January 2025
^{T}} matrix inversion can be reduced to inverting symmetric matrices and 2 additional matrix multiplications, because the positive definite matrix M T...
46 KB (7,006 words) - 17:18, 16 December 2024
distribution with a nonsingular covariance matrix Σ precisely if Σ ∈ Rp × p is a positive-definite matrix and the probability density function of X is...
25 KB (3,930 words) - 21:12, 2 August 2024
mathematics, positive semidefinite may refer to: Positive semidefinite function Positive semidefinite matrix Positive semidefinite quadratic form Positive semidefinite...
227 bytes (53 words) - 17:28, 2 May 2021
Note that the Jacobi method does not converge for every symmetric positive-definite matrix. For example, A = ( 29 2 1 2 6 1 1 1 1 5 ) ⇒ D − 1 ( L + U ) =...
13 KB (2,195 words) - 01:32, 4 January 2025
Wishart distribution (redirect from Wishart matrix)
of probability distributions defined over symmetric, positive-definite random matrices (i.e. matrix-valued random variables). These distributions are of...
27 KB (4,206 words) - 12:06, 10 January 2025
mathematics, particularly matrix theory, a Stieltjes matrix, named after Thomas Joannes Stieltjes, is a real symmetric positive definite matrix with nonpositive...
1 KB (140 words) - 22:54, 5 November 2024
analysis, an incomplete Cholesky factorization of a symmetric positive definite matrix is a sparse approximation of the Cholesky factorization. An incomplete...
11 KB (2,051 words) - 18:10, 19 April 2024
Shear mapping (redirect from Shear matrix)
^{2}&\lambda \\\lambda &1\end{pmatrix}},} which is a positive definite matrix. A typical shear matrix is of the form S = ( 1 0 0 λ 0 0 1 0 0 0 0 0 1 0 0...
13 KB (1,885 words) - 14:31, 26 May 2024
real-valued positive-definite matrices. In Bayesian statistics it can be used as the semi conjugate prior for the covariance matrix or precision matrix of multivariate...
10 KB (1,316 words) - 07:51, 3 June 2024