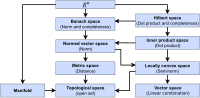
In mathematics, a sesquilinear form is a generalization of a bilinear form that, in turn, is a generalization of the concept of the dot product of Euclidean...

{\displaystyle \mathbf {X} } and Y {\displaystyle \mathbf {Y} } is the sesquilinear form on H 1 × H 2 {\displaystyle H_{1}\times H_{2}} (anti linear in the...

complex numbers C, one is often more interested in sesquilinear forms, which are similar to bilinear forms but are conjugate linear in one argument. Let V...

{\displaystyle \mathbf {x} ^{\mathsf {T}}\mathbf {Ay} ,} and any sesquilinear form may be expressed as x † A y , {\displaystyle \mathbf {x} ^{\dagger...

same way as the canonical norm on the continuous dual space of H). A sesquilinear form is a map B : H × H → C {\displaystyle \mathbb {C} } such that for...

groups of symmetric or skew-symmetric bilinear forms and Hermitian or skew-Hermitian sesquilinear forms defined on real, complex and quaternionic finite-dimensional...

A sesquilinear form φ is reflexive if φ(u, x) = 0 implies φ(x, u) = 0. A duality is a polarity if and only if the (nondegenerate) sesquilinear form defining...

bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: Positive-definite bilinear form Positive-definite...

to consider sesquilinear forms instead of bilinear forms. In that case, a given sesquilinear form ⟨·,·⟩ determines an isomorphism of V with the complex...

{k}}} . Using the bra–ket notation, this space is equipped with a sesquilinear form defined by ⟨ k → a ; ϵ μ | k → b ; ϵ ν ⟩ = ( − η μ ν ) 2 | k → a |...

(disambiguation) Reflections (disambiguation) Reflectivism Sesquilinear form – Generalization of a bilinear form This disambiguation page lists articles associated...

the signature of a form. This should not be confused with the indefinite unitary group U(p, q) which preserves a sesquilinear form of signature (p, q)...

or an alternating form. The definition extends to a bilinear form on a free module over a commutative ring, and to a sesquilinear form extended to include...

{b}}\langle x,z\rangle .} This implies that an inner product is a sesquilinear form. ⟨ x + y , x + y ⟩ = ⟨ x , x ⟩ + 2 Re ⁡ ( ⟨ x , y ⟩ ) + ⟨ y , y ⟩...

(\mathbf {B} )\,.} [citation needed] Like any inner product, it is a sesquilinear form, for four complex-valued matrices A, B, C, D, and two complex numbers...

M\ } being positive definite: The associated sesquilinear form is an inner product The sesquilinear form defined by M {\displaystyle M} is the function...

Λ) such that R is a ring and Λ a form parameter is called form ring. Let M be an R-module and f a J-sesquilinear form on M (i.e., f ( x r , y s ) = r J...

used to show that this sesquilinear form is in fact positive semidefinite. Since positive semidefinite Hermitian sesquilinear forms satisfy the Cauchy–Schwarz...

Hermitian manifold that satisfies specific conditions Hermitian form, a specific sesquilinear form Hermitian function, a complex function whose complex conjugate...

when the representation admits a nondegenerate invariant sesquilinear form, e.g. a hermitian form. Such representations are sometimes said to be complex...

or complex linear space, endowed with a bilinear or respectively sesquilinear form, satisfying some conditions and called an inner product. Every inner...

have a non-trivial invariant sesquilinear form. The problem is that it is in general hard to tell when the quadratic form is positive definite. For many...

product – Mathematical operation on vector spaces Sesquilinear form – Generalization of a bilinear form Bilinear filtering – Method of interpolating functions...

Proof Construction of the Hilbert space H Define on A a semi-definite sesquilinear form ⟨ a , b ⟩ = ρ ( b ∗ a ) , a , b ∈ A . {\displaystyle \langle a,b\rangle...

vector space, one often works with sesquilinear forms (conjugate-linear in one argument) instead of bilinear forms. The Hermitian adjoint of a map between...

matrix, quadratic form, bilinear form, and transpose xT replaced respectively by Hermitian matrix, Hermitian form, sesquilinear form, and conjugate transpose...

the additional structure of an inner product (a conjugate symmetric sesquilinear form) is known as a Hilbert space, which is in some sense a particularly...

antilinear map. It is also assumed that one of the two coordinates of a sesquilinear form has this property (such as the inner product of a Hilbert space)....

)=\langle \xi \mid T\eta \rangle +\langle \xi \mid \eta \rangle } is a sesquilinear form on dom T and Q ⁡ ( ξ , ξ ) = ⟨ ξ ∣ T ξ ⟩ + ⟨ ξ ∣ ξ ⟩ ≥ ‖ ξ ‖ 2 . {\displaystyle...

representations have a nondegenerate invariant sesquilinear form, it is hard to determine when this form is positive definite. An effective description...