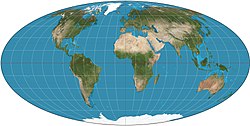
consequence of the Theorema Egregium is that the Earth cannot be displayed on a map without distortion. Gauss's Theorema Egregium (Latin for "Remarkable...

the content of the Theorema Egregium. Gaussian curvature is named after Carl Friedrich Gauss, who published the Theorema Egregium in 1827. At any point...

located in the ambient Euclidean space. The crowning result, the Theorema Egregium of Gauss, established that the Gaussian curvature is an intrinsic...

two theorems of Carl Friedrich Gauss: Theorema Egregium, "Remarkable Theorem", best-known example Aureum Theorema, "Golden Theorem", better-known as quadratic...

maps of the world Rhumbline network – navigational aid drawn on maps Theorema Egregium – a geometric theorem Time zone Large-Scale Distortions in Map Projections...

geometry. One of the oldest such discoveries is Carl Friedrich Gauss's Theorema Egregium ("remarkable theorem") that asserts roughly that the Gaussian curvature...

the Earth's surface onto a flat plane, a consequence of the later Theorema Egregium of Gauss. The first systematic or rigorous treatment of geometry using...

Gauss map in differential geometry Gaussian curvature, defined in his Theorema egregium Gauss circle problem Gauss–Kuzmin–Wirsing constant, a constant in...

two-dimensional being constrained to move on it. As a result, the Theorema Egregium (remarkable theorem), established a property of the notion of Gaussian...

surface (the first fundamental form). This result is known as the Theorema Egregium ("remarkable theorem" in Latin). A map that preserves the local measurements...

differential geometry of surfaces, which Gauss himself proved in his theorema egregium. The fundamental objects are called the Riemannian metric and the...

4D spacetimePages displaying wikidata descriptions as a fallback Theorema Egregium – Differential geometry theorem—The "remarkable theorem" discovered...

L, M, and N are the coefficients of the second fundamental form. Theorema egregium of Gauss states that the Gaussian curvature of a surface can be expressed...

projective geometry; Gergonne point Carl Friedrich Gauss (1777–1855) – Theorema Egregium Louis Poinsot (1777–1859) Siméon Denis Poisson (1781–1840) Jean-Victor...

a layer of paint. Chattel house Metal roof Nissen hut Quonset hut Theorema Egregium, for more information on why corrugation increases strength Tin tabernacle...

– Originally described something that was remarkably good (as in Theorema Egregium). The word is from the Latin egregius "illustrious, select", literally...

change apparent density of the phenomenon being mapped. By Gauss's Theorema Egregium, an equal-area projection cannot be conformal. This implies that an...

differences are reduced to imperceptibility. Carl Friedrich Gauss's Theorema Egregium proved that a sphere's surface cannot be represented on a plane without...

unexpected insights into mathematical structures. For example, Gauss's Theorema Egregium is a deep theorem which relates a local phenomenon (curvature) to...

Gauss equation, as it may be viewed as a generalization of Gauss's Theorema Egregium. For general Riemannian manifolds one has to add the curvature of...

cylinder, which is a consequence of Gaussian curvature and Gauss's Theorema Egregium. A familiar example of this is a floppy pizza slice, which will remain...

constant Gaussian curvature at each point equal to 1/r2. As per Gauss's Theorema Egregium, this curvature is independent of the sphere's embedding in 3-dimensional...

points on the map to a bar scale on the map. As proved by Gauss’s Theorema Egregium, a sphere (or ellipsoid) cannot be projected onto a plane without...

theorem (foliations) Gauss's lemma (riemannian geometry) Gauss's Theorema Egregium (differential geometry) Gauss–Bonnet theorem (differential geometry)...

the Riemannian metric of the surface. This is Gauss's celebrated Theorema Egregium, which he found while concerned with geographic surveys and mapmaking...

Darboux frame Toponogov (2006) This equation is the basis for Gauss's theorema egregium. Gauss 1828. (Kline 1972, p. 885). Peterson (1853) Ivanov 2001. Terminology...

Curvature Radius of curvature Osculating circle Curve Fenchel's theorem Theorema egregium Gauss–Bonnet theorem First fundamental form Second fundamental form...

consider abstract spaces as mathematical objects in their own right. His theorema egregium gives a method for computing the curvature of a surface without considering...

introducing the notion of Gaussian curvature and Gauss's celebrated Theorema Egregium. Bernhard Riemann (1854) Publication data: "Über die Hypothesen, welche...

Gauss curvature of the standard S 2 {\displaystyle S^{2}} , by Gauss' Theorema Egregium. M. W. Hirsch, Immersions of manifold. Trans. Amer. Math. Soc. 93...