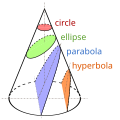
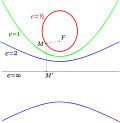
conic sections are called confocal if they have the same foci. Because ellipses and hyperbolas have two foci, there are confocal ellipses, confocal hyperbolas...

A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola...

In geometry, confocal means having the same foci: confocal conic sections. For an optical cavity consisting of two mirrors, confocal means that they share...

spherical conics. For example, Graves's theorem and Ivory's theorem about confocal conics can also be proven on the sphere; see confocal conic sections about...

equation Quadratic function Universal parabolic constant Confocal conic sections § Confocal parabolas The tangential plane just touches the conical surface...

but confocal focaloids of the same mass or charge produce the same action on a test mass or charge in the exterior region. Homoeoid Confocal conic sections...

the horizontal circles and the meridians. The article confocal conic sections deals with confocal quadrics, too. They are a prominent example of a non...

and F2 are the foci of the ellipse in the xy-plane, too. Hence, it is confocal to the given ellipse and the length of the string is l = 2rx + (a − c)...

his published work, such as: "On a Characteristic Property of Confocal Conic Sections" is available (open source) on Project Euclid. Haruki earned his...

one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse...

numerically, for example by Runge–Kutta methods. Cassini oval Confocal conic sections Trajectory Apollonian circles, pairs of families of circles that...

properties of liquid crystals. One should not mix focal conics with confocal conics. The latter ones have all the same foci. Equations If one describes...

is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...

the other two forms of conic sections, parabolas and hyperbolas, both of which are open and unbounded. An angled cross section of a right circular cylinder...

{\displaystyle x^{2}-y^{2}-\lambda xy-1=0,\ \ \ \lambda \in \mathbb {R} .} These conic sections have no points with the y-axis in common and intersect the x-axis at...

of the use of the rectifying latitude is the equidistant conic projection. (Snyder, Section 16). The rectifying latitude is also of great importance in...

(Semple & Roth 1949, p.238, 288). See complex. conic A conic is a degree 2 curve. Short for "conic section", the intersection of a cone with a plane. conjugate...

Mainardi's answer to determining the oblique trajectory of a system of confocal ellipses. He also made lasting contributions in differential geometry,...

Mainardi's answer to determining the oblique trajectory of a system of confocal ellipses. He also made lasting contributions in differential geometry,...