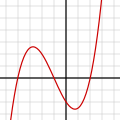
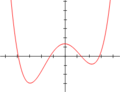
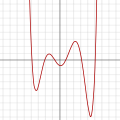In algebra, a cubic equation in one variable is an equation of the form a x 3 + b x 2 + c x + d = 0 {\displaystyle ax^{3}+bx^{2}+cx+d=0} in which a is...

Cubic equations of state are a specific class of thermodynamic models for modeling the pressure of a gas as a function of temperature and density and...

domain is restricted to the real numbers. Setting f(x) = 0 produces a cubic equation of the form a x 3 + b x 2 + c x + d = 0 , {\displaystyle ax^{3}+bx^{2}+cx+d=0...

mathematician who first discovered a method to solve the depressed cubic equation. Scipione del Ferro was born in Bologna, in northern Italy, to Floriano...

quintic and higher-order equations, beyond trivial or special cases. Linear equation Quadratic equation Cubic equation Quintic equation Polynomial Newton's...

In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation ⁠ F ( x , y , z ) = 0 {\displaystyle F(x,y,z)=0} ⁠ applied...

finding Linear equation (degree = 1) Quadratic equation (degree = 2) Cubic equation (degree = 3) Quartic equation (degree = 4) Quintic equation (degree = 5)...

whose roots are also roots of the original polynomial. The general cubic equation a x 3 + b x 2 + c x + d = 0 {\displaystyle ax^{3}+bx^{2}+cx+d=0} with...

is most notable for his work on the classification and solution of cubic equations, where he provided a geometric formulation based on the intersection...

cubic inch Square yard Orders of magnitude (volume) Conversion of units Cube (arithmetic), cube root Cubic equation, cubic function IEEE Std 260.1-2004...

possible except for the depressed equation y4 = 0. Now, if m is a root of the cubic equation such that m ≠ 0, equation (1) becomes ( y 2 + p 2 + m ) 2 =...

study of equations of state, and was the starting point of cubic equations of state, which most famously continued via the Redlich–Kwong equation of state...

Nested radicals appear in the algebraic solution of the cubic equation. Any cubic equation can be written in simplified form without a quadratic term...

Functional equation Functional equation (L-function) Constitutive equation Laws of science Defining equation (physical chemistry) List of equations in classical...

mathematicians of the 16th century to cubic equations that cannot be solved in terms of real radicals, that is to those equations such that the computation of...

linear equation for degree one quadratic equation for degree two cubic equation for degree three quartic equation for degree four quintic equation for degree...

variables. One method of solving the cubic equation involves transforming variables to obtain a sextic equation having terms only of degrees 6, 3, and...

found several solutions of the cubic equation. Omar Khayyam found the general geometric solution of a cubic equation.[citation needed] Omar Khayyam (c...

quadratic equations with positive roots, and many cubic equations, although it is not known if they were able to reduce the general cubic equation. Ancient...

and Joseph Neng Shun Kwong in 1949. It showed that a two-parameter, cubic equation of state could well reflect reality in many situations, standing alongside...

where all vertices have degree 3 Cubic plane curve (mathematics), a plane algebraic curve C defined by a cubic equation Cubic reciprocity (mathematics - number...

the cubic equations by promising not to publish them. Tartaglia divulged the secrets of the solutions of three different forms of the cubic equation in...

2 + k 2 x + k 3 {\displaystyle y(x)=k_{1}x^{2}+k_{2}x+k_{3}} for a cubic equation of degree n = 3 {\displaystyle n=3} , f ( x ) = x 3 + a 2 x 2 + a 1...

of a cubic equation, as he had neither complex numbers at his disposal, nor the algebraic notation to be able to describe a general cubic equation. With...

_{r}+c\rho _{r}^{2}+f\rho _{r}^{5}} The three-term virial equation or a cubic virial equation of state Z = 1 + B ρ + C ρ 2 {\displaystyle Z=1+B\rho +C\rho...

cubic roots for nonzero complex numbers. Rafael Bombelli was the first to address explicitly these seemingly paradoxical solutions of cubic equations...

BCE and commented on by Liu Hui in the 3rd century CE. Cabtaxi number Cubic equation Doubling the cube Eighth power Euler's sum of powers conjecture Fifth...

theory. Solving quadratic equations with continued fractions Linear equation Cubic function Quartic equation Quintic equation Fundamental theorem of algebra...

The Koide formula is an unexplained empirical equation discovered by Yoshio Koide in 1981. In its original form, it is not fully empirical but a set of...

a^{3}-2a^{2}b-ab^{2}+b^{3}=0.} Thus –b/c, c/a, and a/b all satisfy the cubic equation t 3 − 2 t 2 − t + 1 = 0. {\displaystyle t^{3}-2t^{2}-t+1=0.} However...