differential geometry, the curvature form describes curvature of a connection on a principal bundle. The Riemann curvature tensor in Riemannian geometry...
5 KB (884 words) - 23:37, 25 February 2025
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being...
44 KB (6,491 words) - 21:34, 17 June 2025
the manifold a symmetric bilinear form (Besse 1987, p. 43). Broadly, one could analogize the role of the Ricci curvature in Riemannian geometry to that of...
34 KB (5,863 words) - 23:45, 30 December 2024
introduced an abstract and rigorous way to define curvature for these manifolds, now known as the Riemann curvature tensor. Similar notions have found applications...
12 KB (2,115 words) - 00:45, 22 May 2025
The main tensorial invariant of a connection form is its curvature form. In the presence of a solder form identifying the vector bundle with the tangent...
27 KB (4,630 words) - 05:01, 6 January 2025
Spinal column (redirect from Spinal curvature)
(thoracic and sacral curvatures) form during fetal development. The secondary curves develop after birth. The cervical curvature forms as a result of lifting...
43 KB (5,307 words) - 18:16, 6 June 2025
f12 = Ez/c, f23 = −Bz, or equivalent definitions. This form is a special case of the curvature form on the U(1) principal bundle on which both electromagnetism...
67 KB (10,058 words) - 14:15, 26 June 2025
equal to the integral of a certain polynomial (the Euler class) of its curvature form (an analytical invariant). It is a highly non-trivial generalization...
13 KB (1,856 words) - 17:14, 17 June 2025
term curvature tensor may refer to: the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds; the curvature of...
562 bytes (100 words) - 07:37, 14 November 2023
Kähler manifold (redirect from Holomorphic sectional curvature)
metric whose curvature form ω is positive (since ω is then a Kähler form that represents the first Chern class of L in H2(X, Z)). The Kähler form ω that satisfies...
33 KB (4,739 words) - 20:31, 30 April 2025
Gaussian curvature or Gauss curvature Κ of a smooth surface in three-dimensional space at a point is the product of the principal curvatures, κ1 and κ2...
19 KB (2,638 words) - 00:42, 15 April 2025
Torsion tensor (redirect from Torsion form)
Z\right)+R\left(T\left(X,Y\right),Z\right)\right)=0} The curvature form is the gl(n)-valued 2-form Ω = D ω = d ω + ω ∧ ω {\displaystyle \Omega =D\omega =d\omega...
27 KB (4,375 words) - 19:53, 19 June 2025
geometry, the two principal curvatures at a given point of a surface are the maximum and minimum values of the curvature as expressed by the eigenvalues...
10 KB (1,290 words) - 06:48, 1 May 2024
In mathematics, the mean curvature H {\displaystyle H} of a surface S {\displaystyle S} is an extrinsic measure of curvature that comes from differential...
11 KB (1,739 words) - 23:18, 6 April 2025
fundamental form Gauss–Codazzi–Mainardi equations Dupin indicatrix Asymptotic curve Curvature Principal curvatures Mean curvature Gauss curvature Elliptic...
9 KB (682 words) - 03:50, 5 December 2024
Spherical Earth (redirect from Curvature of the earth)
Spherical Earth or Earth's curvature refers to the approximation of the figure of the Earth as a sphere. The earliest documented mention of the concept...
17 KB (1,903 words) - 15:49, 14 May 2025
Pontryagin class (redirect from Pontryagin form)
\mathbf {Q} )} can be presented as differential forms which depend polynomially on the curvature form of a vector bundle. This Chern–Weil theory revealed...
10 KB (1,906 words) - 02:09, 12 April 2025
Connection (principal bundle) (section Curvature form)
{\displaystyle P\times ^{G}W} . The curvature form of a principal G-connection ω is the g {\displaystyle {\mathfrak {g}}} -valued 2-form Ω defined by Ω = d ω + 1...
20 KB (3,436 words) - 15:33, 16 March 2025
formulations of geometric invariants, such as the curvature (see also curvature tensor and curvature form), and torsion tensor. Consider the following problem...
19 KB (2,617 words) - 17:10, 15 March 2025
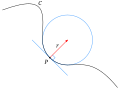
Osculating circle (redirect from Circle of curvature)
best approximates the curvature of a curve at a specific point. It is tangent to the curve at that point and has the same curvature as the curve at that...
19 KB (3,358 words) - 14:06, 7 January 2025
geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional...
20 KB (3,104 words) - 17:02, 18 February 2025
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno...
19 KB (2,934 words) - 18:43, 20 December 2024
in terms of connections and curvature representing classes in the de Rham cohomology rings of M. That is, the theory forms a bridge between the areas of...
15 KB (2,782 words) - 06:37, 9 March 2025
nondegenerate bilinear form over g {\displaystyle {\mathfrak {g}}} (if G is semisimple, the Killing form will do) and F is the curvature form F ≡ d A + A ∧ A...
3 KB (394 words) - 10:52, 29 April 2025
one can write down concretely any k-form of the closed connection ω as some 2k-form of the associated curvature form Ω of ω. In 1974 S. S. Chern and J....
27 KB (3,591 words) - 12:48, 25 May 2025
mathematical field of Riemannian geometry, the scalar curvature (or the Ricci scalar) is a measure of the curvature of a Riemannian manifold. To each point on a...
35 KB (5,036 words) - 15:53, 12 June 2025
Earth radius (redirect from Earth radius of curvature)
and measure the Earth's radius involve either the spheroid's radius of curvature or the actual topography. A few definitions yield values outside the range...
42 KB (4,474 words) - 20:57, 9 June 2025
fundamental form, it serves to define extrinsic invariants of the surface, its principal curvatures. More generally, such a quadratic form is defined for...
10 KB (1,444 words) - 10:13, 17 March 2025
Connection (vector bundle) (section Curvature)
}\wedge \sigma .} A flat connection is one whose curvature form vanishes identically. The curvature form has a local description called Cartan's structure...
45 KB (8,674 words) - 13:23, 15 June 2025
classes can be expressed as polynomials in the coefficients of the curvature form. There are various ways of approaching the subject, each of which focuses...
42 KB (7,508 words) - 13:07, 21 April 2025