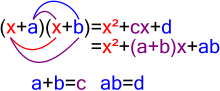In mathematics, the nth cyclotomic polynomial, for any positive integer n, is the unique irreducible polynomial with integer coefficients that is a divisor...

geometric fact accounts for the term "cyclotomic" in such phrases as cyclotomic field and cyclotomic polynomial; it is from the Greek roots "cyclo" (circle)...

_{n})} of Q {\displaystyle \mathbb {Q} } generated by ζn. The nth cyclotomic polynomial Φ n ( x ) = ∏ gcd ( k , n ) = 1 1 ≤ k ≤ n ( x − e 2 π i k / n )...

denominator, 1 − z j, which is the product of cyclotomic polynomials. The left hand side of the cyclotomic identity is the generating function for the free...

important class of polynomials whose irreducibility can be established using Eisenstein's criterion is that of the cyclotomic polynomials for prime numbers...

All-one polynomials Abel polynomials Bell polynomials Bernoulli polynomials Cyclotomic polynomials Dickson polynomials Fibonacci polynomials Lagrange...

irreducible cyclotomic polynomials", Electronics and Communications in Japan, 74 (4): 106–113, doi:10.1002/ecjc.4430740412, MR 1136200. all one polynomial at PlanetMath...

coprime to p, the roots of the nth cyclotomic polynomial are distinct in every field of characteristic p, as this polynomial is a divisor of Xn − 1, whose...

function φ(n) in number theory; also called Euler's phi function. The cyclotomic polynomial functions Φn(x) of algebra. The number of electrical phases in a...

number i is X 2 + 1 {\displaystyle X^{2}+1} . The cyclotomic polynomials are the minimal polynomials of the roots of unity. In linear algebra, the n×n...

Brahmagupta polynomials Caloric polynomial Charlier polynomials Chebyshev polynomials Chihara–Ismail polynomials Cyclotomic polynomials Dickson polynomial Ehrhart...

unity. Then the minimal polynomial of ζ n {\displaystyle \zeta _{n}} is given by the n {\displaystyle n} -th cyclotomic polynomial Φ n ( x ) {\displaystyle...

of certain integer values of the cyclotomic polynomials. Because cyclotomic polynomials are irreducible polynomials over the integers, such a factorization...

of palindromic polynomials include cyclotomic polynomials and Eulerian polynomials. If a is a root of a polynomial that is either palindromic or antipalindromic...

and mathematics Cyclotomic polynomial – Irreducible polynomial whose roots are nth roots of unity Diophantine equation – Polynomial equation whose integer...

class of examples comes from the splitting fields of cyclotomic polynomials. These are polynomials Φ n {\displaystyle \Phi _{n}} defined as Φ n ( x ) =...

evidence it is not known that this sequence extends indefinitely. The cyclotomic polynomials Φ k ( x ) {\displaystyle \Phi _{k}(x)} for k = 1 , 2 , 3 , … {\displaystyle...

not divide n, and Q n ( x ) {\displaystyle Q_{n}(x)} is the nth cyclotomic polynomial. For example, a 6 − b 6 = Q ¯ 1 ( a , b ) Q ¯ 2 ( a , b ) Q ¯ 3...

{\displaystyle \Phi _{d}(x)} is the d t h {\displaystyle d^{\mathrm {th} }} cyclotomic polynomial and d ranges over the divisors of n. For p prime, Φ p ( x ) = ∑...

Equivalently, a regular n-gon is constructible if any root of the nth cyclotomic polynomial is constructible. Restating the Gauss–Wantzel theorem: A regular...

the fourth cyclotomic polynomial. As with the cyclotomic polynomials more generally, Φ 4 {\displaystyle \Phi _{4}} is an irreducible polynomial, so this...

upper bound and what is known to be attained through cyclotomic polynomials. Cyclotomic polynomials cannot close this gap by a result of Bateman that states...

those associated with the cyclotomic polynomials of degrees 5 and 17. Charles Hermite, on the other hand, showed that polynomials of degree 5 are solvable...

modulo p is also equivalent to finding the roots of the (p − 1)st cyclotomic polynomial modulo p. The least primitive root gp modulo p (in the range 1,...

measure of an irreducible non-cyclotomic polynomial. Lehmer's polynomial is a factor of the shorter degree-12 polynomial, Q ( x ) = x 12 − x 7 − x 6 −...

factors of xn − 1 appears to be the same as the height of the nth cyclotomic polynomial. This was shown by computer to be true for n < 10000 and was expected...

primitive roots of unity; they are the roots of the nth cyclotomic polynomial. For example, the polynomial z3 − 1 factors as (z − 1)(z − ω)(z − ω2), where ω...

has a prime factor p such that any kth cyclotomic polynomial Φk(p) is smooth. The first few cyclotomic polynomials are given by the sequence Φ1(p) = p−1...

prime Emma Lehmer, "On the magnitude of the coefficients of the cyclotomic polynomial", Bulletin of the American Mathematical Society 42 (1936), no. 6...

2, the polynomial Φ(x) will be the cyclotomic polynomial xn + 1. Other choices of n are possible but the corresponding cyclotomic polynomials are more...