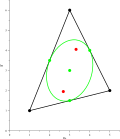
segment of this line. The Gauss–Lucas theorem, named after Carl Friedrich Gauss and Félix Lucas, is similar in spirit to Rolle's theorem. If P is a (nonconstant)...

Ostrogradsky–Gauss theorem Gauss pseudospectral method Gauss transform, also known as Weierstrass transform. Gauss–Lucas theorem Gauss's continued fraction...

size of p, that is the sum of the bitsize of its coefficients. The Gauss–Lucas theorem states that the convex hull of the roots of a polynomial contains...

rational root theorem is a special case (for a single linear factor) of Gauss's lemma on the factorization of polynomials. The integral root theorem is the special...

version, see Voorhoeve index. Mean value theorem Intermediate value theorem Linear interpolation Gauss–Lucas theorem Besenyei, A. (September 17, 2012). "A...

Descartes' rule of signs Newton's identities Gauss–Lucas theorem Properties of polynomial roots Rational root theorem Symmetric polynomial and elementary symmetric...

Riemann–Roch theorem. Argument principle Control theory § Stability Filter design Filter (signal processing) Gauss–Lucas theorem Hurwitz's theorem (complex...

theorem Hurwitz's theorem (complex analysis) Descartes' rule of signs Rouché's theorem Properties of polynomial roots Gauss–Lucas theorem Turán's inequalities...

form a triangle, and the Gauss–Lucas theorem states that the roots of its derivative lie within this triangle. Marden's theorem states their location within...

a distance no more than 1 from at least one critical point. The Gauss–Lucas theorem says that all of the critical points lie within the convex hull of...

its roots. Convex hulls and polynomials also come together in the Gauss–Lucas theorem, according to which the roots of the derivative of a polynomial all...

its zeros in | z | < 1 {\displaystyle |z|<1} . By virtue of the Gauss–Lucas theorem, P ′ ( z ) + ε   Q ′ ( z ) {\displaystyle P'(z)+\varepsilon \ Q'(z)}...

Gamas's Theorem (multilinear algebra) Gauss's Theorema Egregium (differential geometry) Gauss–Bonnet theorem (differential geometry) Gauss–Lucas theorem (complex...

point because it is not included in the function's domain. By the Gauss–Lucas theorem, all of a polynomial function's critical points in the complex plane...

polynomial roots – Geometry of the location of polynomial roots Gauss–Lucas theorem – Geometric relation between the roots of a polynomial and those...

Fermat numbers (1877), Proth's theorem (c. 1878), the Lucas–Lehmer primality test (originated 1856), and the generalized Lucas primality test. Since 1951...

gave a full proof of necessity in 1837. The result is known as the Gauss–Wantzel theorem: An n-sided regular polygon can be constructed with compass and...

theorem Wilson's theorem Primitive root modulo n Multiplicative order Discrete logarithm Quadratic residue Euler's criterion Legendre symbol Gauss's lemma...

a new geometry. Gauss wrote in an 1824 letter to Franz Taurinus that he had constructed it, but Gauss did not publish his work. Gauss called it "non-Euclidean...

determination of the sign of the Gauss sum, the investigations into biquadratic reciprocity, and unpublished notes. Gauss, Carl Friedrich (1801), Disquisitiones...

as of September 2022[update]. The conjecture terminology may persist: theorems often enough may still be referred to as conjectures, using the anachronistic...

number operations in geometrical terms. 1799 – Carl Friedrich Gauss proves the fundamental theorem of algebra (every polynomial equation has a solution among...

Constructible number Complex conjugate root theorem Algebraic element Horner scheme Rational root theorem Gauss's lemma (polynomial) Irreducible polynomial...

"Variational Analysis of the Abscissa Mapping for Polynomials via the Gauss-Lucas Theorem". Journal of Global Optimization. 28 (3/4): 259–268. doi:10.1023/B:JOGO...

divergence theorem earlier described by Lagrange, Gauss and Green, 1841 - Karl Weierstrass discovers but does not publish the Laurent expansion theorem, 1843...

n} by induction. The German mathematician and scientist, Carl Friedrich Gauss, is said to have found this relationship in his early youth, by multiplying...

Carl Gauss used the Euclidean algorithm to demonstrate unique factorization of Gaussian integers, although his work was first published in 1832. Gauss mentioned...

characteristic function and Hamilton–Jacobi equation 1829 - Carl Friedrich Gauss introduces Gauss's principle of least constraint 1834 - Carl Jacobi discovers his...

Gause's principle – Georgii Gause Gauss's law – Carl Friedrich Gauss Gauss–Bonnet gravity, theorem – Carl Friedrich Gauss and Pierre Ossian Bonnet Geib–Spevack...

same for the three elements). The name is derived from the Pythagorean theorem, stating that every right triangle has side lengths satisfying the formula...