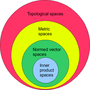
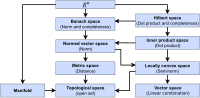
an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product...

product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically...

function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that induces a distance function for which the space is a complete...

indefinite inner product space ( K , ⟨ ⋅ , ⋅ ⟩ , J ) {\displaystyle (K,\langle \cdot ,\,\cdot \rangle ,J)} is an infinite-dimensional complex vector space K {\displaystyle...

semidirect products Product of rings Ideal operations, for product of ideals Scalar multiplication Matrix multiplication Inner product, on an inner product space...

Mirror (2022) Priam InnerSpace, a hard disk drive series by Priam Corporation in the 1980s Inner product space, a kind of vector space in linear algebra...

vector space equipped with the usual dot product ⟨ ⋅ , ⋅ ⟩ {\displaystyle \langle \cdot ,\cdot \rangle } (thus making it an inner product space), and let...

specifically a Hilbert space, because the space is complete under the metric induced by the inner product. This inner product space is conventionally denoted...

complete for this norm. An inner product space is a normed vector space whose norm is the square root of the inner product of a vector and itself. The...

inequality) is an upper bound on the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered...

2\|x\|^{2}+2\|y\|^{2}\quad {\text{ for all }}x,y.} In an inner product space, the norm is determined using the inner product: ‖ x ‖ 2 = ⟨ x , x ⟩ . {\displaystyle \|x\|^{2}=\langle...

mathematics, particularly linear algebra, an orthonormal basis for an inner product space V {\displaystyle V} with finite dimension is a basis for V {\displaystyle...

inner product for Euclidean vector spaces, better known as the dot product. The dot product is the trace of the outer product. Unlike the dot product...

conditions and called an inner product. Every inner product space is also a normed space. A normed space underlies an inner product space if and only if it satisfies...

a linear transformation is analogous to the null space of a matrix. If V is an inner product space, then the orthogonal complement to the kernel can...

with infinitely many components in an inner product space, as in functional analysis. In an inner product space, the concept of perpendicularity is replaced...

defined over a set of labels S {\displaystyle S} in an inner product space with an inner product ⟨ ⋅ , ⋅ ⟩ {\displaystyle \langle \cdot ,\cdot \rangle...

tensor product. The tensor product allows Hilbert spaces to be collected into a symmetric monoidal category. Since Hilbert spaces have inner products, one...

of an inner product. Physical space can be modelled as a vector space which additionally has the structure of an inner product. The inner product defines...

generally in any inner product space, and whenever it is true for a real normed vector space, that space must be an inner product space. For other types...

translations which is equipped with an inner product. The action of translations makes the space an affine space, and this allows defining lines, planes...

vectors defined in an inner product space. Cosine similarity is the cosine of the angle between the vectors; that is, it is the dot product of the vectors divided...

. {\displaystyle \{{\vec {x}}\}^{\perp }.} For example, taking the inner product with a fixed function g ∈ L 2 ( [ − π , π ] ) {\displaystyle g\in L^{2}([-\pi...

strictly positive. A semi-inner-product, L-semi-inner product, or a semi-inner product in the sense of Lumer for a linear vector space V {\displaystyle V} over...

in an orthonormal basis over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued...

The isosceles triangle theorem holds in inner product spaces over the real or complex numbers. In such spaces, given vectors x, y, and z, the theorem...

an inner product ( ⋅ , ⋅ ) {\displaystyle (\cdot ,\cdot )} with antilinear first argument, which makes V {\displaystyle V} an inner product space. Then...

of topological vector spaces, which include function spaces, inner product spaces, normed spaces, Hilbert spaces and Banach spaces. In this article, vectors...

function space. The inner product space is then called complete. A complete inner product space is a Hilbert space. The abstract state space is always...

space, allowing two vectors to be multiplied in the defined way to produce a scalar. A vector space equipped with a scalar product is called an inner...