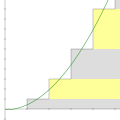
In mathematics and theoretical physics, zeta function regularization is a type of regularization or summability method that assigns finite values to divergent...

values even to a divergent series. In particular, the methods of zeta function regularization and Ramanujan summation assign the series a value of ⁠−+1/12⁠...

methods for obtaining values from divergent series, including zeta function regularization. 1 + 1 + 1 + 1 + ⋯ is a divergent series, meaning that its sequence...

dimensional regularization can be used to study the physics of crystals that macroscopically appear to be fractals. It has been argued that zeta function regularization...

then its value at s = −1 is called the zeta regularized sum of the series a1 + a2 + ... Zeta function regularization is nonlinear. In applications, the numbers...

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined...

regularization Lattice regularization Pauli–Villars regularization Zeldovich regularization Zeta function regularization Perturbative predictions by quantum field...

mathematics, Hadamard regularization (also called Hadamard finite part or Hadamard's partie finie) is a method of regularizing divergent integrals by...

regularization is more difficult to use in QCD calculations. P–V serves as a helpful alternative to the more commonly used dimensional regularization...

regularization Lattice regularization Zeta function regularization Causal perturbation theory Hadamard regularization Point-splitting regularization v...

x^{m-2r}=-{\frac {a^{m-2r+1}}{m-2r+1}}.} Note that this involves (see zeta function regularization) I ( n , Λ ) = ∫ 0 Λ d x x n {\displaystyle I(n,\Lambda )=\int...

^{2}}{6\gamma }}\end{aligned}}} also hold true. The digamma function appears in the regularization of divergent integrals ∫ 0 ∞ d x x + a , {\displaystyle...

first case, the multiplication is determined with some regularization of generalized function. In the second case, the algebra is constructed as multiplication...

Renormalization group UV fixed point Causal perturbation theory Zeta function regularization J.D. Bjorken, S. Drell (1965). Relativistic Quantum Fields, Preface...

perform some kind of regularization. The most popular of which for computing functional determinants is the zeta function regularization. For instance, this...

diagram calculations into the counterterms. When using dimensional regularization, i.e. d 4 p → μ 4 − d d d p {\displaystyle d^{4}p\to \mu ^{4-d}d^{d}p}...

Riemann zeta function is a function in complex analysis, which is also important in number theory. It is often denoted ζ ( s ) {\displaystyle \zeta (s)}...

inspiration for later attempts at regularization and renormalization in quantum field theory. (See also regularization (physics) for an alternative way...

_{N}^{\infty }{\frac {S_{f}(y)}{y^{s+1}}}dy.} General Dirichlet series Zeta function regularization Euler product Dirichlet convolution The formulas for both series...

where the left-hand side of the equation is the two-point correlation function of the Dirac field. In a new theory, the Dirac field can interact with...

reference. Quantum triviality Scale invariance Schröder's equation Regularization (physics) Density matrix renormalization group Functional renormalization...

Probability-generating function Star transform Zak transform Zeta function regularization Mandal, Jyotsna Kumar (2020). "Z-Transform-Based Reversible Encoding"...

Hilbert–Pólya conjecture states that the non-trivial zeros of the Riemann zeta function correspond to eigenvalues of a self-adjoint operator. It is a possible...

of the Riemann zeta function and Dirichlet beta function.: 137  In connection to the Laplace and Mellin transform. In the regularization/renormalization...

practice both numbers are often infinite so are defined using zeta function regularization. It was introduced by Atiyah, Patodi, and Singer (1973, 1975)...

In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a function e r f : C → C {\displaystyle \mathrm {erf}...

Roger (1979), "Irrationalité de ζ ( 2 ) {\displaystyle \zeta (2)} et ζ ( 3 ) {\displaystyle \zeta (3)} ", Astérisque, 61: 11–13. Kingdom of Infinite Number:...

field theory String cosmology Supergravity The Elegant Universe Zeta function regularization Sen, Ashoke (1999-12-29). "Universality of the tachyon potential"...

equivalent to empirical risk minimization with Tikhonov regularization, where in this case the loss function is the hinge loss ℓ ( y , z ) = max ( 0 , 1 − y z...

ultraviolet divergences in the corresponding calculations. From the generalized functions point of view, the problem of divergences is rooted in the fact that the...