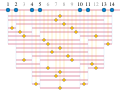
An arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference from any succeeding term to its preceding term remains...
13 KB (2,312 words) - 05:55, 29 June 2025
arithmetic progression, the sum of the reciprocals of the prime numbers in the progression diverges and that different such arithmetic progressions with...
24 KB (3,526 words) - 22:13, 17 June 2025
mathematics, a generalized arithmetic progression (or multiple arithmetic progression) is a generalization of an arithmetic progression equipped with multiple...
3 KB (548 words) - 04:04, 20 November 2024
primes in arithmetic progression are any sequence of at least three prime numbers that are consecutive terms in an arithmetic progression. An example...
17 KB (1,832 words) - 23:48, 24 May 2025
positive integers by taking as a base a suitable collection of arithmetic progressions, sequences of the form { b , b + a , b + 2 a , . . . } {\displaystyle...
13 KB (1,732 words) - 07:37, 24 May 2025
Magic square (redirect from The Arithmetic Progression in Magic square)
of s arithmetic progressions with the same common difference among r terms, such that r × s = n2, and whose initial terms are also in arithmetic progression...
276 KB (21,821 words) - 00:47, 7 July 2025
Prime number theorem (redirect from Prime number theorem for arithmetic progressions)
Erdős–Selberg argument". Let πd,a(x) denote the number of primes in the arithmetic progression a, a + d, a + 2d, a + 3d, ... that are less than x. Dirichlet and...
66 KB (9,149 words) - 10:47, 6 July 2025
yields a geometric progression, while taking the logarithm of each term in a geometric progression yields an arithmetic progression. The relation that...
9 KB (1,594 words) - 09:00, 1 June 2025
mathematics, a harmonic progression (or harmonic sequence) is a progression formed by taking the reciprocals of an arithmetic progression, which is also known...
5 KB (699 words) - 21:17, 14 April 2025
Roth's theorem on arithmetic progressions is a result in additive combinatorics concerning the existence of arithmetic progressions in subsets of the...
28 KB (4,555 words) - 11:10, 9 May 2025
Prime number (section Arithmetic progressions)
19th century result was Dirichlet's theorem on arithmetic progressions, that certain arithmetic progressions contain infinitely many primes. Many mathematicians...
117 KB (14,179 words) - 23:31, 23 June 2025
Erdős' conjecture on arithmetic progressions, often referred to as the Erdős–Turán conjecture, is a conjecture in arithmetic combinatorics (not to be...
7 KB (895 words) - 05:10, 5 May 2025
In arithmetic combinatorics, Szemerédi's theorem is a result concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured...
22 KB (2,490 words) - 14:21, 12 January 2025
The arithmetic progression game is a positional game where two players alternately pick numbers, trying to occupy a complete arithmetic progression of...
2 KB (327 words) - 02:40, 6 December 2024
arbitrarily long arithmetic progressions. In other words, for every natural number k {\displaystyle k} , there exist arithmetic progressions of primes with...
13 KB (1,538 words) - 17:30, 10 March 2025
numbers in an arithmetic progression of three squares. The congruum problem is the problem of finding squares in arithmetic progression and their associated...
9 KB (1,135 words) - 01:43, 22 May 2025
Klaus Roth (section Arithmetic combinatorics)
approximation, Roth made major contributions to the theory of progression-free sets in arithmetic combinatorics and to the theory of irregularities of distribution...
30 KB (3,359 words) - 23:15, 1 April 2025
in particular in arithmetic combinatorics, a Salem-Spencer set is a set of numbers no three of which form an arithmetic progression. Salem–Spencer sets...
22 KB (2,612 words) - 18:21, 10 October 2024
Look up progression in Wiktionary, the free dictionary. Progression may refer to: In mathematics: Arithmetic progression, a sequence of numbers such that...
2 KB (299 words) - 15:42, 25 August 2024
number of numbers in the collection. Arithmetic progression In mathematics, an arithmetic progression (AP) or arithmetic sequence is a sequence of numbers...
279 KB (31,753 words) - 08:50, 12 July 2025
Number theory (redirect from Higher arithmetic)
of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties...
81 KB (9,977 words) - 15:36, 28 June 2025
Problems involving arithmetic progressions are of interest in number theory, combinatorics, and computer science, both from theoretical and applied points...
5 KB (622 words) - 21:18, 14 April 2025
edge, the energy is the sum of an arithmetic progression, and using the formula for the sum of an arithmetic progression, one can show that E ( Z ) ≤ T (...
27 KB (3,634 words) - 13:58, 2 July 2025
the same color form an arithmetic progression. But you can't add a ninth integer to the end without creating such a progression. If you add a red 9, then...
30 KB (3,690 words) - 13:24, 24 May 2025
one of r different colors, then there are at least k integers in arithmetic progression all of the same color. The smallest such N is the van der Waerden...
22 KB (1,121 words) - 21:24, 26 January 2025
Arithmetico-geometric sequence (redirect from Arithmetico-geometric progression)
multiplication of the elements of a geometric progression with the corresponding elements of an arithmetic progression. The nth element of an arithmetico-geometric...
10 KB (2,160 words) - 00:46, 21 June 2025
temperatures), which he labels by two systems, one in arithmetic progression and the other in geometric progression, as follows: Outline of metrology and measurement...
7 KB (582 words) - 13:57, 1 July 2025
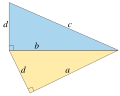
Fermat's right triangle theorem (category Arithmetic problems of plane geometry)
If three square numbers form an arithmetic progression, then the gap between consecutive numbers in the progression (called a congruum) cannot itself...
16 KB (2,279 words) - 04:11, 14 May 2025
_{i=0}^{n}i=\sum _{i=1}^{n}i={\frac {n(n+1)}{2}}\qquad } (Sum of the simplest arithmetic progression, consisting of the first n natural numbers.): 52 ∑ i = 1 n ( 2...
26 KB (4,940 words) - 08:56, 28 June 2025
Cube (algebra) (redirect from Cube (arithmetic))
In arithmetic and algebra, the cube of a number n is its third power, that is, the result of multiplying three instances of n together. The cube of a number...
24 KB (3,032 words) - 16:41, 16 May 2025