to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters)...

In mathematics, particularly in dynamical systems, a bifurcation diagram shows the values visited or approached asymptotically (fixed points, periodic...

In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation where the system transitions from...

In mathematics, specifically bifurcation theory, the Feigenbaum constants /ˈfaɪɡənbaʊm/ δ and α are two mathematical constants which both express ratios...

bifurcations called a Hopf bifurcation and an infinite period bifurcation.[citation needed] Biological applications of bifurcation theory Biophysics Biostatistics...

differential equations, bifurcation theory and the calculus of variations. He is currently a professor in the Department of Mathematics, Cornell University...

The Hopf bifurcation is a two-dimensional analog of the pitchfork bifurcation. Many different kinds of systems exhibit Hopf bifurcations, from radio...

constant δ is the limiting ratio of each bifurcation interval to the next between every period-doubling bifurcation. The logistic map is a polynomial mapping...

E(k)<25^{k^{2}}} . Arnold's_Problems#Notable_problems Bifurcation theory Limit cycle List of unsolved problems in mathematics A similar interpretation can be found in...

In the mathematical area of bifurcation theory a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two...

{p}{q}}} is known as a bifurcation: the attracting fixed point "collides" with a repelling period-q cycle. As we pass through the bifurcation parameter into the...

qualitatively and the dynamical system is said to have gone through a bifurcation. Bifurcation theory considers a structure in phase space (typically a fixed...

set theory and mathematical logic. Contents:  Top A B C D E F G H I J K L M N O P Q R S T U V W X Y Z See also References Bifurcation theory the study...

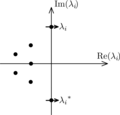
In bifurcation theory, a field within mathematics, a Bogdanov–Takens bifurcation is a well-studied example of a bifurcation with co-dimension two, meaning...

In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general...

increasing rate Hopf bifurcation, in mathematics, a local bifurcation; when the first Lyapunov coefficient is negative, the bifurcation is called supercritical...

of a tree are bifurcation ratios, numbers describing how close to balanced a tree is. For each order i in a hierarchy, the ith bifurcation ratio is n i...

topologically equivalent to the normal form of the bifurcation. For example, the normal form of a saddle-node bifurcation is d x d t = μ + x 2 {\displaystyle {\frac...

the bifurcation locus can be thought of as an analog of the Julia set in parameter space. Without doubt, the most famous example of a bifurcation locus...

chaotic dynamics. Mathematics portal Systems science portal Examples of chaotic systems Advected contours Arnold's cat map Bifurcation theory Bouncing ball...

In bifurcation theory, a field within mathematics, a transcritical bifurcation is a particular kind of local bifurcation, meaning that it is characterized...

A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a symbol (e.g., an alphabet letter), or...

successive period-doubling bifurcations occur tends to a constant of around 4.6692... He was able to provide a mathematical argument of that fact, and...

was created in 2017 after bifurcation from Lower Subansiri district. Kra Daadi district was created in 2015 after bifurcation from Kurung Kumey district...

systems at local points. Borges anticipated the development of bifurcation theory in mathematics, through "The Garden of Forking Paths" in 1941. In "Garden"...

In dynamical systems theory, a period-doubling bifurcation occurs when a slight change in a system's parameters causes a new periodic trajectory to emerge...

achievements in mathematics. These include mathematical research, mathematics education,: xii  the history and philosophy of mathematics, public outreach...

(including Veterinary). AP EAPCET is being held since 1986. After the bifurcation of Andhra Pradesh, TG EAPCET is being held separately in Telangana, since...

high-contrast black-and-white reversal film. The title refers to the mathematical constant pi. The story focuses on a mathematician with an obsession to...

SciSearch) ISI Alerting Services Mathematical Reviews INSPEC Zentralblatt MATH "International Journal of Bifurcation and Chaos in Applied Sciences and...