In category theory, a category is Cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified...
18 KB (2,611 words) - 01:50, 26 March 2025
Cartesian closed categories are closed categories. In particular, any topos is closed. The canonical example is the category of sets. Compact closed categories...
3 KB (348 words) - 12:41, 19 March 2025
in category theory, a closed monoidal category (or a monoidal closed category) is a category that is both a monoidal category and a closed category in...
7 KB (1,167 words) - 18:33, 17 September 2023
Any category with finite products (a "finite product category") can be thought of as a cartesian monoidal category. In any cartesian monoidal category, the...
5 KB (571 words) - 12:40, 10 May 2025
and CPO, the category of complete partial orders with Scott-continuous functions. A topos is a certain type of cartesian closed category in which all...
21 KB (2,525 words) - 18:54, 19 March 2025
product; thus any category with a Cartesian product (and a final object) is a Cartesian closed category. In graph theory, the Cartesian product of two graphs...
27 KB (3,945 words) - 17:31, 22 April 2025
value Inverse limit – Construction in category theory Cartesian closed category – Type of category in category theory Categorical pullback – Most general...
14 KB (2,401 words) - 21:09, 27 March 2025
a closed category in category theory Cartesian coordinate system, modern rectangular coordinate system Cartesian diagram, a construction in category theory...
2 KB (257 words) - 10:25, 1 June 2023
Dual (category theory) Groupoid Image (category theory) Coimage Commutative diagram Cartesian morphism Slice category Isomorphism of categories Natural...
5 KB (402 words) - 15:20, 29 March 2024
being a Cartesian closed category while still containing all of the typical spaces of interest. This makes CGHaus a particularly convenient category of topological...
11 KB (1,365 words) - 23:19, 14 May 2025
theory, where a cartesian closed category is taken as a non-syntactic description of a lambda calculus. At the very least, category theoretic language...
34 KB (3,910 words) - 19:56, 5 July 2025
to the corresponding free categories: F : Quiv → Cat Cat has all small limits and colimits. Cat is a Cartesian closed category, with exponential D C {\displaystyle...
3 KB (268 words) - 23:18, 14 May 2025
in category theory, where it is right adjoint to currying in closed monoidal categories. A special case of this are the Cartesian closed categories, whose...
12 KB (1,449 words) - 17:58, 29 March 2025
Exponential object (redirect from Exponential (category theory))
all finite products and exponential objects are called cartesian closed categories. Categories (such as subcategories of Top) without adjoined products...
8 KB (1,143 words) - 18:49, 9 October 2024
bifunctor. Cartesian closed category – Type of category in category theory Limits and colimits in an ∞-category Mac Lane, Saunders (1998). Categories for the...
27 KB (4,333 words) - 16:33, 22 June 2025
is Rel, the category having sets as objects and relations as morphisms, with Cartesian monoidal structure. A symmetric monoidal category ( C , ⊗ , I )...
9 KB (1,678 words) - 08:55, 26 October 2024
Examples include cartesian closed categories such as Set, the category of sets, and compact closed categories such as FdVect, the category of finite-dimensional...
18 KB (2,436 words) - 07:41, 19 June 2025
Compactly generated space (redirect from K-closed set)
shortcomings of the category of topological spaces. In particular, under some of the definitions, they form a cartesian closed category while still containing...
30 KB (4,641 words) - 15:25, 21 April 2025
typed lambda calculus and cartesian closed categories. Under this correspondence, objects of a cartesian-closed category can be interpreted as propositions...
58 KB (6,386 words) - 00:10, 10 June 2025
Adjoint functors (redirect from Unit (category theory))
the indiscrete category on that set. Exponential object. In a cartesian closed category the endofunctor C → C given by –×A has a right adjoint –A. This...
64 KB (10,260 words) - 08:58, 28 May 2025
category, a distributive lattice as a small posetal distributive category, a Heyting algebra as a small posetal finitely cocomplete cartesian closed category...
3 KB (320 words) - 16:17, 21 May 2025
equivalence F is an exact functor. C is a cartesian closed category (or a topos) if and only if D is cartesian closed (or a topos). Dualities "turn all concepts...
14 KB (1,986 words) - 16:35, 23 March 2025
Lambda calculus (category Commons category link from Wikidata)
objects in the style of the lambda calculus Cartesian closed category – A setting for lambda calculus in category theory Categorical abstract machine – A...
90 KB (12,115 words) - 02:49, 7 July 2025
Currying (section Category theory)
objects). Categories that do have both products and internal homs are exactly the closed monoidal categories. The setting of cartesian closed categories is sufficient...
36 KB (5,036 words) - 09:11, 23 June 2025
. The category Cat {\displaystyle {\textbf {Cat}}} of all small categories with functors as morphisms is therefore a cartesian closed category. Mathematics...
11 KB (1,776 words) - 18:31, 16 May 2025
A category is said to be locally cartesian closed if every slice of it is cartesian closed (see above for the notion of slice). Locally cartesian closed...
17 KB (2,870 words) - 19:30, 8 October 2024
In category theory, a branch of mathematics, dagger compact categories (or dagger compact closed categories) first appeared in 1989 in the work of Sergio...
15 KB (2,010 words) - 21:23, 9 February 2025
functions taken as morphisms, and the cartesian product taken as the product, forms a Cartesian closed category. Here, eval (or, properly speaking, apply)...
24 KB (2,948 words) - 14:04, 3 July 2025
non-examples of symmetric monoidal categories: The category of sets. The tensor product is the set theoretic cartesian product, and any singleton can be...
5 KB (631 words) - 00:45, 10 July 2023
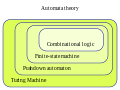
Automata theory (section Category-theoretic models)
automata homomorphisms defining the arrows between automata is a Cartesian closed category, it has both categorical limits and colimits. An automata homomorphism...
32 KB (3,851 words) - 10:11, 30 June 2025