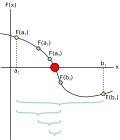
In mathematical analysis, the intermediate value theorem states that if f {\displaystyle f} is a continuous function whose domain contains the interval...

b])), this is a consequence of the intermediate value theorem. But even when ƒ′ is not continuous, Darboux's theorem places a severe restriction on what...

completeness given above. The intermediate value theorem states that every continuous function that attains both negative and positive values has a root. This is...

analysis, such as the intermediate value theorem, the Bolzano–Weierstrass theorem, the extreme value theorem, and the Heine–Borel theorem. It is usually taken...

power of Robinson's approach, a short proof of the intermediate value theorem (Bolzano's theorem) using infinitesimals is done by the following. Let...

} The intermediate value theorem is an existence theorem, based on the real number property of completeness, and states: If the real-valued function...

covered by the line changes continuously from 0 to 1, so by the intermediate value theorem it must be equal to 1/2 somewhere along the way. It is possible...

spaces. Some theorems can only be formulated in terms of approximations. For a simple example, consider the intermediate value theorem (IVT). In classical...

considered found. These generally use the intermediate value theorem, which asserts that if a continuous function has values of opposite signs at the end points...

a function and complex analysis, proved the intermediate value theorem and the Bolzano–Weierstrass theorem, and used the latter to study the properties...

least one real root. That fact can also be proved by using the intermediate value theorem. The polynomial x2 + 1 = 0 has roots ± i. Any real square matrix...

In mathematics, the Poincaré–Miranda theorem is a generalization of intermediate value theorem, from a single function in a single dimension, to n functions...

calculus, Rolle's theorem or Rolle's lemma essentially states that any real-valued differentiable function that attains equal values at two distinct points...

Brouwer fixed-point theorem follows almost immediately from the intermediate value theorem. Another example of toy theorem is Rolle's theorem, which is obtained...

hairy ball theorem implies that there is no single continuous function that accomplishes this task. Fixed-point theorem Intermediate value theorem Vector...

the converse of the intermediate value theorem. In other words, it is a function that satisfies a particular intermediate-value property — on any interval...

proof of the intermediate value theorem (also known as Bolzano's theorem). Today he is mostly remembered for the Bolzano–Weierstrass theorem, which Karl...

first proved by Bolzano in 1817 as a lemma in the proof of the intermediate value theorem. Some fifty years later the result was identified as significant...

{\displaystyle [x-\delta ,x+\delta ]\subseteq (x_{0}-r,x_{0}+r)} . By the intermediate value theorem, we find that f {\displaystyle f} maps the interval [ x − δ ,...

provided a non-analytic proof of his intermediate value theorem and then, several years later provided a proof of the theorem that was free from intuitions concerning...

implicitly in the epsilon-delta definition of continuity; the intermediate value theorem asserts that the image of an interval by a continuous function...

unit interval is a fixed point space, as can be proved from the intermediate value theorem. The real line is not a fixed-point space, because the continuous...

require only a small amount of analysis (more precisely, the intermediate value theorem in both cases): every polynomial with an odd degree and real coefficients...

theorem Goodstein's theorem Green's theorem (to do) Green's theorem when D is a simple region Heine–Borel theorem Intermediate value theorem Itô's lemma Kőnig's...

In this case a and b are said to bracket a root since, by the intermediate value theorem, the continuous function f must have at least one root in the...

F making it an ordered field such that, in this ordering, the intermediate value theorem holds for all polynomials over F with degree ≥ 0. F is a weakly...

which maps x to f(x) − x. It is ≥ 0 on a and ≤ 0 on b. By the intermediate value theorem, g has a zero in [a, b]; this zero is a fixed point. Brouwer is...

{b-a}{n}}\right)} The intermediate value theorems gives us c such that g ( c ) = 0 {\displaystyle g(c)=0} and the theorem follows. Intermediate value theorem Borsuk–Ulam...

been acknowledged by Weierstrass's followers. Stevin proved the intermediate value theorem for polynomials, anticipating Cauchy's proof thereof. Stevin uses...

analysis, such as the monotone convergence theorem, the intermediate value theorem and the mean value theorem. However, while the results in real analysis...