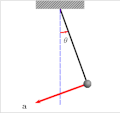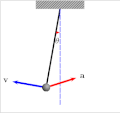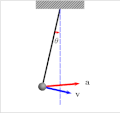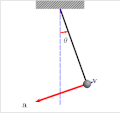
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least...

relativistic Lagrangian mechanics is Lagrangian mechanics applied in the context of special relativity and general relativity. The relativistic Lagrangian can...

Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces...

Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used...

case one may revert to Newtonian mechanics. Two dominant branches of analytical mechanics are Lagrangian mechanics (using generalized coordinates and...

In classical mechanics, Routh's procedure or Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by...

density Lagrangian mechanics, a formulation of classical mechanics Lagrangian (field theory), a formalism in classical field theory Lagrangian point, a...

of energy Lagrangian mechanics, another theoretical formalism, based on the principle of the least action Classical statistical mechanics generalizes...

In mathematics, the inverse problem for Lagrangian mechanics is the problem of determining whether a given system of ordinary differential equations can...

of Y → X. In classical mechanics, many dynamical systems are Lagrangian systems. The configuration space of such a Lagrangian system is a fiber bundle...

derivation of (Eq. 1) Equation 1 can additionally be obtained through Lagrangian Mechanics. More specifically, using the Euler–Lagrange equations (or Lagrange's...

Functional derivative Functional integration Hamiltonian mechanics Lagrangian Lagrangian mechanics Measure (physics) Noether's theorem Path integral formulation...

to the conservation of angular momentum throughout the motion. In Lagrangian mechanics, angular momentum for rotation around a given axis, is the conjugate...

T^{*}Q} ; these coordinates are called the canonical coordinates. In Lagrangian mechanics, a different set of coordinates are used, called the generalized...

leading to the development of analytical mechanics (which includes Lagrangian mechanics and Hamiltonian mechanics). These advances, made predominantly in...

Semisprays arise naturally as the extremal curves of action integrals in Lagrangian mechanics. Generalizing all these examples, any (possibly nonlinear) connection...

translational symmetry. Advanced formulations of classical mechanics, Lagrangian and Hamiltonian mechanics, allow one to choose coordinate systems that incorporate...

variational problem for a functional based on a single function, the Lagrangian, which may contain all physical information concerning the system and...

Broglie relation is not true in a crystal. Most often in Lagrangian mechanics, the Lagrangian L(q, dq/dt, t) is in configuration space, where q = (q1,...

concepts. One of these instances occurs in Lagrangian mechanics. Lagrangian mechanics formulates mechanics in terms of generalized coordinates {qk}, which...

a theorem of Mikhail Ostrogradsky in classical mechanics according to which a non-degenerate Lagrangian dependent on time derivatives higher than the first...

Lagrangian optics are two formulations of geometrical optics which share much of the mathematical formalism with Hamiltonian mechanics and Lagrangian...

Hamiltonian constraint Moment map Contact geometry Analysis of flows Nambu mechanics Action (physics) Lagrangian Euler–Lagrange equations Noether's theorem...

classical mechanics through quantum mechanics, particle physics, and general relativity. Action principles start with an energy function called a Lagrangian describing...

}}} Incorporating Lagrangian mechanics and using the Euler–Lagrange equation, Christoffel symbols can be substituted into the Lagrangian to account for the...

T={\tfrac {1}{2}}mv^{2}} and potential V {\displaystyle V} parts of the Lagrangian L = T − V {\displaystyle L=T-V} in arbitrary generalized coordinates the...

Displacement field (mechanics) Equivalent latitude Generalized Lagrangian mean Trajectory (fluid mechanics) Liouville's theorem (Hamiltonian) Lagrangian particle...

reformulation of the original problem, known as the Lagrangian function or Lagrangian. In the general case, the Lagrangian is defined as L ( x , λ ) ≡ f ( x ) + ⟨...

In celestial mechanics, the Lagrange points (/ləˈɡrɑːndʒ/; also Lagrangian points or libration points) are points of equilibrium for small-mass objects...

zero-thickness (infinitely thin) string behaviour, using the principles of Lagrangian mechanics. Just as the action for a free point particle is proportional to...