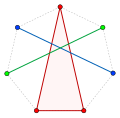
In geometry, Radon's theorem on convex sets, published by Johann Radon in 1921, states that: Any set of d + 2 points in Rd can be partitioned into two...

In mathematics, the Radon–Nikodym theorem is a result in measure theory that expresses the relationship between two measures defined on the same measurable...

nonempty intersection. We prove the finite version, using Radon's theorem as in the proof by Radon (1921). The infinite version then follows by the finite...

classical problem of differential topology, beginning with the hairy ball theorem, and early work on the classification of division algebras. Specifically...

reconstruction); Radon's theorem, that d + 2 points in d dimensions may always be partitioned into two subsets with intersecting convex hulls; the Radon–Hurwitz...

theorem is known as a Tverberg partition. The special case r = 2 {\displaystyle r=2} was proved earlier by Radon, and it is known as Radon's theorem....

Pizza theorem (geometry) Radon's theorem (convex sets) Separating axis theorem (convex geometry) Steinitz theorem (graph theory) Stewart's theorem (plane...

Helly's theorem Kirchberger's theorem N-dimensional polyhedron Radon's theorem, and its generalization Tverberg's theorem Krein–Milman theorem Choquet...

Bayes' theorem (alternatively Bayes' law or Bayes' rule, after Thomas Bayes) gives a mathematical rule for inverting conditional probabilities, allowing...

the Radon transform. Cauchy–Crofton theorem is a closely related formula for computing the length of curves in space. Fast Fourier transform Radon 1917...

analysis and convex analysis Helly's theorem – Theorem about the intersections of d-dimensional convex sets Radon's theorem – Says d+2 points in d dimensions...

1 , n , n ) {\displaystyle \;(1,n,n)\;} is admissible. The Hurwitz–Radon theorem states that ( ρ ( n ) , n , n ) {\displaystyle \;\left(\rho (n),n,n\right)\;}...

measures or regular Borel measures or Radon measures or signed measures or complex measures. The statement of the theorem for positive linear functionals on...

Holomorphically convex hull Integrally-convex set John ellipsoid Pseudoconvexity Radon's theorem Shapley–Folkman lemma Symmetric set Morris, Carla C.; Stark, Robert...

1090/surv/015. ISBN 978-0-8218-1515-1. (See Theorem II.2.6) Bárcenas, Diómedes (2003). "The Radon–Nikodym Theorem for Reflexive Banach Spaces" (PDF). Divulgaciones...

Girsanov's theorem or the Cameron-Martin-Girsanov theorem explains how stochastic processes change under changes in measure. The theorem is especially...

In mathematics, Hurwitz's theorem is a theorem of Adolf Hurwitz (1859–1919), published posthumously in 1923, solving the Hurwitz problem for finite-dimensional...

can be shattered). However, no set of 4 points can be shattered: by Radon's theorem, any four points can be partitioned into two subsets with intersecting...

tool for understanding the behaviour of polynomials over local fields Radon's theorem - on convex sets, that any set of d + 2 points in Rd can be partitioned...

Russo–Dye theorem describes the convex hulls of unitary elements in a C*-algebra. In discrete geometry, both Radon's theorem and Tverberg's theorem concern...

In mathematics, the projection-slice theorem, central slice theorem or Fourier slice theorem in two dimensions states that the results of the following...

Wiener–Khinchin theorem or Wiener–Khintchine theorem, also known as the Wiener–Khinchin–Einstein theorem or the Khinchin–Kolmogorov theorem, states that...

In mathematics, Stinespring's dilation theorem, also called Stinespring's factorization theorem, named after W. Forrest Stinespring, is a result from operator...

theorem, Carathéodory's theorem, and Radon's theorem all postdate Kirchberger's theorem. A strengthened version of Kirchberger's theorem fixes one of the given...

representation theorem, each positive linear form on K(X) arises as integration with respect to a unique regular Borel measure. A real-valued Radon measure is...

singular). Lebesgue's decomposition theorem can be refined in a number of ways. First, as the Lebesgue-Radon-Nikodym theorem. That is, let ( Ω , Σ ) {\displaystyle...

generalization of Choi's theorem is known as Belavkin's "Radon–Nikodym" theorem for completely positive maps. Choi's theorem. Let Φ : C n × n → C m ×...

Many results—Carathéodory's theorem, Helly's theorem, Radon's theorem, the Hahn–Banach theorem, the Krein–Milman theorem, the lemma of Farkas—can be formulated...

extension theorem (also known as Kolmogorov existence theorem, the Kolmogorov consistency theorem or the Daniell-Kolmogorov theorem) is a theorem that guarantees...

(In fact, there is a unique translation invariant Radon measure up to scale by Haar's theorem: the n {\displaystyle n} -dimensional Lebesgue measure...