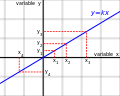
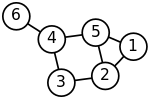
In mathematics, a relation denotes some kind of relationship between two objects in a set, which may or may not hold. As an example, "is less than" is...

In mathematics, a binary relation associates elements of one set called the domain with elements of another set called the codomain. Precisely, a binary...

a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the dispersion relation, one can calculate the...

physical system A finitary or n-ary relation is a set of n-tuples. Specific types of relations include: Relation (mathematics) (an elementary treatment of binary...

In mathematics, a binary relation R {\displaystyle R} on a set X {\displaystyle X} is reflexive if it relates every element of X {\displaystyle X} to itself...

In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most...

In mathematics, a binary relation R on a set X is transitive if, for all elements a, b, c in X, whenever R relates a to b and b to c, then R also relates...

In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments...

In mathematics, a finitary relation over a sequence of sets X1, ..., Xn is a subset of the Cartesian product X1 × ... × Xn; that is, it is a set of n-tuples...

{\displaystyle {\stackrel {?}{=}}} symbol. An equivalence relation is a mathematical relation that generalizes the idea of similarity or sameness. It is...

The relationship between mathematics and physics has been a subject of study of philosophers, mathematicians and physicists since antiquity, and more...

In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant...

for mathematical statements Relation – Relationship between two sets, defined by a set of ordered pairs For further reading in discrete mathematics, beyond...

In mathematics, a binary relation R {\displaystyle R} on a set X {\displaystyle X} is antisymmetric if there is no pair of distinct elements of X {\displaystyle...

In mathematics, a recurrence relation is an equation according to which the n {\displaystyle n} th term of a sequence of numbers is equal to some combination...

In mathematics, an element (or member) of a set is any one of the distinct objects that belong to that set. For example, given a set called A containing...

In mathematics, a tuple is a finite sequence or ordered list of numbers or, more generally, mathematical objects, which are called the elements of the...

Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection...

In mathematics, a homogeneous relation (also called endorelation) on a set X is a binary relation between X and itself, i.e. it is a subset of the Cartesian...

logic, mathematics, and computer science, arity (/ˈærɪti/ ) is the number of arguments or operands taken by a function, operation or relation. In mathematics...

In mathematics, a set is a collection of different things; these things are called elements or members of the set and are typically mathematical objects...

), and when defining a mathematical function as a relation from one set (the domain) to another set (the range). Mathematics portal Glossary of set theory...

correspondences are bijections between sets of mathematical objects of apparently very different nature. For a binary relation pairing elements of set X with elements...

In mathematics, a partial equivalence relation (often abbreviated as PER, in older literature also called restricted equivalence relation) is a homogeneous...

A symmetric relation is a type of binary relation. Formally, a binary relation R over a set X is symmetric if: ∀ a , b ∈ X ( a R b ⇔ b R a ) , {\displaystyle...

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences...

include the philosophical study of the relation of this framework with reality. The term "foundations of mathematics" was not coined before the end of the...

In mathematics, an asymmetric relation is a binary relation R {\displaystyle R} on a set X {\displaystyle X} where for all a , b ∈ X , {\displaystyle a...

In mathematics, a set A is a subset of a set B if all elements of A are also elements of B; B is then a superset of A. It is possible for A and B to be...

In mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...