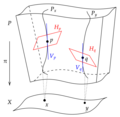
Ehresmann connection (after the French mathematician Charles Ehresmann who first formalized this concept) is a version of the notion of a connection,...

introduction of the concepts of Ehresmann connection and of jet bundles, and for his seminar on category theory. Ehresmann was born in Strasbourg (at the...

principal connection can be viewed as a special case of the notion of an Ehresmann connection, and is sometimes called a principal Ehresmann connection. It...

the connection, the marked points given by s always move under parallel transport. Yet another way to define a Cartan connection is with an Ehresmann connection...

connection is a way of formulating some aspects of connection theory using differential forms and Lie groups. An Ehresmann connection is a connection...

model Klein geometry Ehresmann connection, gives a manner for differentiating sections of a general fibre bundle Electrical connection, allows the flow of...

defining connections. In fact, the following notion of "Ehresmann connection" is nothing but an infinitesimal formulation of parallel transport. (Ehresmann connection)...

is enough that the connection be equivariant under positive rescalings: it need not be linear. That is, (cf. Ehresmann connection#Vector bundles and covariant...

(Koszul or linear Ehresmann) connection on a vector bundle. Originally the term affine connection is short for an affine connection in the sense of Cartan...

}g^{-1}-(dg)g^{-1}.} A connection on a vector bundle may be specified similarly to the case for principal bundles above, known as an Ehresmann connection. However vector...

a vector on M, and d denotes the pushforward. Ehresmann connection Cartan connection Affine connection Curvature form Griffiths & Harris (1978), Wells...

integrable. An Ehresmann connection on E is a choice of a complementary subbundle HE to VE in TE, called the horizontal bundle of the connection. At each point...

{\mathfrak {g}}} , and P → B be a principal G-bundle. Let ω be an Ehresmann connection on P (which is a g {\displaystyle {\mathfrak {g}}} -valued one-form...

vectors in much the same way as with a covariant derivative. An Ehresmann or Cartan connection supplies a lifting of curves from the manifold to the total...

sequence 1. A connection always exists. Sometimes, this connection Γ is called the Ehresmann connection because it yields the horizontal distribution H Y =...

language, an Ehresmann connection) and formulating all rates of change in terms of the covariant derivative with respect to this connection. The gauge field...

the Gauss–Manin connection constructed in a manner analogous to that in which the Ehresmann connection generalizes the Koszul connection. The construction...

an affine connection or covariant derivative (on tensors); the curvature form of an Ehresmann connection: see Ehresmann connection, connection (principal...

linear connection on the tangent bundle of a manifold. In older literature, the term linear connection is occasionally used for an Ehresmann connection or...

Einstein–Cartan theory connection (vector bundle) connection (principal bundle) Ehresmann connection curvature curvature form holonomy, local holonomy...

understanding of differential forms, Charles Ehresmann who introduced the theory of fibre bundles and Ehresmann connections, and others. Of particular importance...

surface isometric to the plane. Dilation same as Lipschitz constant. Ehresmann connection Einstein manifold Euclidean geometry Exponential map Exponential...

essentially to Charles Ehresmann. However, it is different from, though related to, what is commonly called an Ehresmann connection. It is also different...

needed to add to an arbitrary connection to get the torsion-free Levi-Civita connection. That is, given an Ehresmann connection ω {\displaystyle \omega }...

and the triple (TE, p∗, TM) is a smooth vector bundle. The general Ehresmann connection TE = HE ⊕ VE on a vector bundle (E, p, M) can be characterized in...

A μ {\displaystyle A_{\mu }} is interpreted as the gauge connection (the Ehresmann connection) on the circle bundle. This geometric interpretation then...

Differential form – Expression that may be integrated over a region Ehresmann connection – Differential geometry construct on fiber bundles Fréchet derivative –...

{\displaystyle H} on a smooth manifold M {\displaystyle M} defines an Ehresmann-connection T ( T M ∖ 0 ) = H ( T M ∖ 0 ) ⊕ V ( T M ∖ 0 ) {\displaystyle T(TM\setminus...

T(TM\setminus 0)=H(TM\setminus 0)\oplus V(TM\setminus 0)} be an Ehresmann connection on the slit tangent bundle TM\0 and consider the mapping D : ( T...

differentiable manifold. It is useful in the study of connections, notably the Ehresmann connection, as well as in the more general study of projections...