In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted E 2 {\displaystyle {\textbf {E}}^{2}} or E 2 {\displaystyle \mathbb {E}...

those is the parallel postulate which relates to parallel lines on a Euclidean plane. Although many of Euclid's results had been stated earlier, Euclid...

In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical...

In Euclidean geometry, a plane is a flat two-dimensional surface that extends indefinitely. Euclidean planes often arise as subspaces of three-dimensional...

two-dimensional Euclidean space, the definite article is used, so the Euclidean plane refers to the whole space. Several notions of a plane may be defined...

distance from a point to a line, in the Euclidean plane The distance from a point to a plane in three-dimensional Euclidean space The distance between two lines...

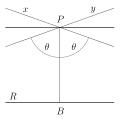
a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: For any given line R and point P not on R, in the plane containing...

geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras...

commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that...

floors. More formally, a tessellation or tiling is a cover of the Euclidean plane by a countable number of closed sets, called tiles, such that the tiles...

non-Euclidean geometry, the Poincaré half-plane model is a way of representing the hyperbolic plane using points in the familiar Euclidean plane. Specifically...

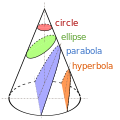
Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as...

a plane, then it is called a hyperbolic plane. q|U is degenerate. One of the most jarring properties (for a Euclidean intuition) of pseudo-Euclidean vectors...

the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles...

⁠, is a two-dimensional projective space, similar to the familiar Euclidean plane in many respects but without the concepts of distance, circles, angle...

Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler...

coordinates of the points of a Euclidean space of dimension n, En (Euclidean line, E; Euclidean plane, E2; Euclidean three-dimensional space, E3) form...

three mutually perpendicular planes. More generally, n Cartesian coordinates specify the point in an n-dimensional Euclidean space for any dimension n....

sphere geometry Non-Euclidean geometry Noncommutative algebraic geometry Noncommutative geometry Ordered geometry Parabolic geometry Plane geometry Projective...

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system...

In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space E n {\displaystyle \mathbb {E} ^{n}} ; that is, the transformations...

tools of spherical trigonometry are in many respects analogous to Euclidean plane geometry and trigonometry, but also have some important differences...

into a correlation, the Euclidean plane (which is not a projective plane) needs to be expanded to the extended euclidean plane by adding a line at infinity...

mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect...

In mathematics, a plane curve is a curve in a plane that may be a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases...

groups and wallpaper groups of the Euclidean plane ( E 2 {\displaystyle E^{2}} ), and their analogues on the hyperbolic plane ( H 2 {\displaystyle H^{2}} )...

represent physical positions, like an affine plane or complex plane. The most basic example is the flat Euclidean plane, an idealization of a flat surface in...

geometry has a variety of properties that differ from those of classical Euclidean plane geometry. For example, the sum of the interior angles of any triangle...

of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space....

In Euclidean geometry, two-dimensional rotations and reflections are two kinds of Euclidean plane isometries which are related to one another. A rotation...