Friedrich Gauss, the integral is ∫ − ∞ ∞ e − x 2 d x = π . {\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}.} Abraham de Moivre originally...
21 KB (4,365 words) - 06:30, 29 May 2025
the Wald distribution Gauss code – described on website of University of Toronto Gauss linking integral (knot theory) Gauss's algorithm for determination...
14 KB (1,117 words) - 16:38, 23 January 2025
Johann Carl Friedrich Gauss (/ɡaʊs/ ; German: Gauß [kaʁl ˈfʁiːdʁɪç ˈɡaʊs] ; Latin: Carolus Fridericus Gauss; 30 April 1777 – 23 February 1855) was a German...
181 KB (17,941 words) - 14:40, 8 July 2025
In electromagnetism, Gauss's law, also known as Gauss's flux theorem or sometimes Gauss's theorem, is one of Maxwell's equations. It is an application...
27 KB (3,806 words) - 15:43, 1 June 2025
Hypergeometric function (redirect from Gauss's hypergeometric theorem)
Euler, but the first full systematic treatment was given by Carl Friedrich Gauss (1813). Studies in the nineteenth century included those of Ernst Kummer (1836)...
38 KB (6,920 words) - 21:17, 14 April 2025
Divergence theorem (redirect from Gauss' theorem)
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem relating the flux of a vector field...
45 KB (7,538 words) - 18:50, 5 July 2025
modified, as elaborated below.) Gauss's law for magnetism can be written in two forms, a differential form and an integral form. These forms are equivalent...
13 KB (1,439 words) - 07:06, 2 July 2024
Maxwell's equations (section Gauss's law)
formulation of Gauss equation up to a trivial rearrangement. Similarly rewriting the magnetic flux in Gauss's law for magnetism in integral form gives ∮...
76 KB (7,991 words) - 23:17, 26 June 2025
mathematics, the Chern theorem (or the Chern–Gauss–Bonnet theorem after Shiing-Shen Chern, Carl Friedrich Gauss, and Pierre Ossian Bonnet) states that the...
13 KB (1,856 words) - 17:14, 17 June 2025
Friedrich Gauss. It states that the flux (surface integral) of the gravitational field over any closed surface is proportional to the mass enclosed. Gauss's law...
15 KB (2,228 words) - 22:32, 26 April 2025
denotes the double factorial. In terms of the Gauss hypergeometric function, the complete elliptic integral of the first kind can be expressed as K ( k...
40 KB (7,831 words) - 04:28, 20 June 2025
them in the 1960s, and Carl Friedrich Gauss. The problem in numerical integration is to approximate definite integrals of the form ∫ a b f ( x ) d x . {\displaystyle...
8 KB (906 words) - 04:37, 14 June 2025
Numerical integration (redirect from Integral approximation)
quadrature rules, such as Gauss-Hermite quadrature for integrals on the whole real line and Gauss-Laguerre quadrature for integrals on the positive reals...
23 KB (3,263 words) - 19:28, 24 June 2025
Gamma function (redirect from Gamma integral)
to have considered the factorial of a complex number, as instead Gauss first did. Gauss also proved the multiplication theorem of the gamma function and...
90 KB (13,547 words) - 17:59, 24 June 2025
Error function (redirect from Gauss error function)
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a function e r f : C → C {\displaystyle \mathrm {erf}...
48 KB (7,340 words) - 13:25, 22 June 2025
setup Schwarz integral formula Parseval–Gutzmer formula Bochner–Martinelli formula Helffer–Sjöstrand formula Titchmarsh 1939, p. 84 "Gauss's Mean-Value Theorem"...
25 KB (4,364 words) - 04:10, 17 May 2025
Fundamental theorem of algebra (redirect from D'Alembert–Gauss theorem)
theorem of algebra, also called d'Alembert's theorem or the d'Alembert–Gauss theorem, states that every non-constant single-variable polynomial with...
51 KB (7,637 words) - 03:42, 7 June 2025
of integrals on algebraic manifolds: Summary of main results and discussion of open problems (Gives a quick sketch of main structure theorem of Gauss–Manin...
8 KB (1,100 words) - 09:13, 28 May 2025
Digamma function (redirect from Gauss's digamma theorem)
is positive then the digamma function has the following integral representation due to Gauss: ψ ( z ) = ∫ 0 ∞ ( e − t t − e − z t 1 − e − t ) d t . {\displaystyle...
36 KB (7,155 words) - 10:49, 14 April 2025
Bernhard Riemann (category CS1 German-language sources (de))
studying mathematics under Carl Friedrich Gauss (specifically his lectures on the method of least squares). Gauss recommended that Riemann give up his theological...
26 KB (2,926 words) - 16:58, 21 March 2025
Lemniscate constant (redirect from Gauss's constant)
the lemniscate constant. Gauss's constant, denoted by G, is equal to ϖ /π ≈ 0.8346268 and named after Carl Friedrich Gauss, who calculated it via the...
31 KB (5,923 words) - 13:55, 4 July 2025
be points on C {\displaystyle C} . Then the writhe is equal to the Gauss integral Wr = 1 4 π ∫ C ∫ C d r 1 × d r 2 ⋅ r 1 − r 2 | r 1 − r 2 | 3 {\displaystyle...
10 KB (1,465 words) - 11:50, 12 September 2024
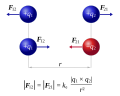
Coulomb's law (redirect from Charles De Coulomb's Law)
if the charge is in motion). Outline of proof Taking S in the integral form of Gauss's law to be a spherical surface of radius r, centered at the point...
42 KB (6,695 words) - 05:13, 7 July 2025
squares, and was the first to officially publish on it, though Carl Friedrich Gauss had discovered it before him. Adrien-Marie Legendre was born in Paris on...
18 KB (1,865 words) - 13:40, 30 June 2025
Sophie Germain (section Correspondence with Gauss)
Braunschweig, where Gauss lived. Germain, concerned that he might suffer the fate of Archimedes, wrote to General Pernety (Joseph Marie de Pernety), a family...
38 KB (4,706 words) - 05:23, 10 June 2025
approximating function, the logarithmic integral li(x) (under the slightly different form of a series, which he communicated to Gauss). Both Legendre's and Dirichlet's...
66 KB (9,149 words) - 10:47, 6 July 2025
the German school of mathematical thinking, under which Carl Friedrich Gauss and his followers largely determined the lines on which mathematics developed...
5 KB (432 words) - 13:32, 21 April 2025
Curve Fenchel's theorem Theorema egregium Gauss–Bonnet theorem First fundamental form Second fundamental form Gauss–Codazzi–Mainardi equations Dupin indicatrix...
9 KB (682 words) - 03:50, 5 December 2024
Differential geometry of surfaces (section Christoffel symbols, Gauss–Codazzi equations, and the Theorema Egregium)
integral of the curvature over the whole surface. As a special case of what is now called the Gauss–Bonnet theorem, Gauss proved that this integral was...
129 KB (17,641 words) - 09:51, 24 June 2025
Electrostatics (section Gauss's law)
considering a Gaussian surface around a body. Mathematically, Gauss's law takes the form of an integral equation: Φ E = ∮ S E ⋅ d A = Q enclosed ε 0 = ∫ V ρ ε...
19 KB (2,620 words) - 09:32, 20 June 2025