In geometry, circle packing is the study of the arrangement of circles (of equal or varying sizes) on a given surface such that no overlapping occurs...
11 KB (1,315 words) - 01:47, 19 April 2025
Circle packing in a circle is a two-dimensional packing problem with the objective of packing unit circles into the smallest possible larger circle. If...
7 KB (370 words) - 07:36, 12 November 2024
Circle packing in a square is a packing problem in recreational mathematics where the aim is to pack n unit circles into the smallest possible square...
5 KB (271 words) - 11:00, 4 March 2025
squares can be packed into some larger shape, often a square or circle. Square packing in a square is the problem of determining the maximum number of...
11 KB (1,189 words) - 22:27, 19 February 2025
The circle packing theorem (also known as the Koebe–Andreev–Thurston theorem) describes the possible tangency relations between circles in the plane whose...
30 KB (3,857 words) - 17:30, 23 June 2025
distinct from the ideas in the circle packing theorem. The related circle packing problem deals with packing circles, possibly of different sizes, on...
22 KB (2,676 words) - 07:08, 25 April 2025
to Circle Packing: The Theory of Discrete Analytic Functions is a mathematical monograph concerning systems of tangent circles and the circle packing theorem...
7 KB (801 words) - 07:26, 14 August 2023
sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions (where the problem becomes circle packing in two dimensions...
29 KB (3,458 words) - 03:40, 30 June 2025
is the three-dimensional equivalent of the circle packing in a circle problem in two dimensions. Best packing of m>1 equal spheres in a sphere setting a...
3 KB (58 words) - 00:34, 21 June 2024
amount n of unit circles can be packed into? More unsolved problems in mathematics Circle packing in an equilateral triangle is a packing problem in discrete...
6 KB (392 words) - 21:06, 21 January 2025
Trihexagonal tiling (section Circle packing)
as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 4 other circles in the packing (kissing...
16 KB (1,625 words) - 23:23, 26 February 2025
It is also related to the densest circle packing of the plane, in which every circle is tangent to six other circles, which fill just over 90% of the area...
4 KB (571 words) - 08:46, 29 June 2025
Snub square tiling (section Circle packing)
as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing...
8 KB (595 words) - 04:03, 26 February 2025
Hexagonal tiling (section Circle packing)
is p6m. If a circle is inscribed in each hexagon, the resulting figure is the densest way to arrange circles in two dimensions; its packing density is π...
20 KB (1,603 words) - 22:05, 3 May 2025
Steinitz's theorem (section Circle packing)
system and lifting the result into three dimensions, or by using the circle packing theorem. Several extensions of the theorem are known, in which the polyhedron...
50 KB (5,973 words) - 06:51, 27 May 2025
Circle packing – Field of geometry closely arranging circles on a plane Circle packing in a circle – Two-dimensional packing problem Circle packing in...
12 KB (2,421 words) - 20:44, 10 March 2025
Truncated trihexagonal tiling (section Circle packing)
as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 3 other circles in the packing (kissing...
10 KB (739 words) - 20:34, 9 June 2025
Ring lemma (category Circle packing)
geometry of circle packings in the Euclidean plane, the ring lemma gives a lower bound on the sizes of adjacent circles in a circle packing. The lemma...
6 KB (693 words) - 18:06, 23 August 2024
even when the locations are fixed. Circle packing in a rectangle Square packing in a square De Bruijn's theorem: packing congruent rectangular bricks of...
7 KB (949 words) - 22:09, 19 June 2025
Snub trihexagonal tiling (section Circle packing)
as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing...
11 KB (814 words) - 22:07, 12 December 2023
Colin L.; Wilks, Allan R.; Yan, Catherine H. (2003), "Apollonian circle packings: number theory", Journal of Number Theory, 100 (1): 1–45, arXiv:math...
11 KB (1,506 words) - 08:26, 22 December 2024
Truncated square tiling (section Circle packing)
as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 3 other circles in the packing (kissing...
8 KB (711 words) - 05:03, 21 January 2025
allocations is referred to as the 'circle-packing' or 'polygon-packing'. Using optimization algorithms, a circle-packing figure can be computed for any uniaxial...
44 KB (5,316 words) - 15:32, 12 May 2025
Apollonian gasket (redirect from Apollonian packing)
circle packing is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles,...
27 KB (2,896 words) - 20:34, 23 June 2025
Truncated hexagonal tiling (section Circle packing)
as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 3 other circles in the packing (kissing...
9 KB (745 words) - 19:46, 6 March 2025
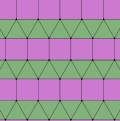
Elongated triangular tiling (section Circle packing)
as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing...
10 KB (700 words) - 21:55, 12 December 2023
set of Kleinian groups; see also Circle packing theorem. The circles of Apollonius may also denote three special circles C 1 , C 2 , C 3 {\displaystyle...
15 KB (2,411 words) - 00:41, 22 May 2025
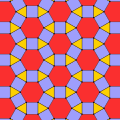
Rhombitrihexagonal tiling (section Circle packing)
as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with four other circles in the packing (kissing...
12 KB (922 words) - 08:48, 25 November 2024
Inversive distance (section Circle packings)
This concept generalizes the circle packings described by the circle packing theorem, in which specified pairs of circles are tangent to each other. Although...
8 KB (1,083 words) - 18:59, 5 September 2024
numbers appear in the ring lemma, used to prove connections between the circle packing theorem and conformal maps. The Fibonacci numbers are important in computational...
86 KB (13,094 words) - 07:08, 5 July 2025