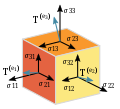
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold M (such as a surface)...

differentiable manifold M {\displaystyle M} and the metric tensor is given as a covariant, second-degree, symmetric tensor on M {\displaystyle M} , conventionally...

(electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), and general relativity (stress–energy tensor, curvature tensor, ...). In...

In multilinear algebra, a tensor contraction is an operation on a tensor that arises from the canonical pairing of a vector space and its dual. In components...

In mathematics, tensor calculus, tensor analysis, or Ricci calculus is an extension of vector calculus to tensor fields (tensors that may vary over a manifold...

geometry of a given metric tensor differs locally from that of ordinary Euclidean space or pseudo-Euclidean space. The Ricci tensor can be characterized...

Minkowski metric η is the metric tensor of Minkowski space. It is a pseudo-Euclidean metric, or more generally, a constant pseudo-Riemannian metric in Cartesian...

the Riemann tensor. This tensor has the same symmetries as the Riemann tensor, but satisfies the extra condition that it is trace-free: metric contraction...

space A metric tensor, in differential geometry, which allows defining lengths of curves, angles, and distances in a manifold Metric tensor (general relativity)...

Eddington–Finkelstein form of the Schwarzschild metric. In the Kerr–Schild form of the Kerr metric, the determinant of the metric tensor is everywhere equal to negative...

by how the tangent space is attached to the cotangent space by the metric tensor. Abstractly, one would say that the manifold has an associated (orthonormal)...

stress-energy tensor The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity...

through the metric tensor, which is a tensor field with one tensor at each point of the space-time manifold, and each belonging to the tensor product of...

the Einstein tensor, g μ ν {\displaystyle g_{\mu \nu }} is the metric tensor, T μ ν {\displaystyle T_{\mu \nu }} is the stress–energy tensor, Λ {\displaystyle...

called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian...

metric (FLRW), where it corresponds to an increase in the scale of the spatial part of the universe's spacetime metric tensor (which governs...

are independent of any metric tensor and coordinate system. Also, the specific term "symbol" emphasizes that it is not a tensor because of how it transforms...

In mathematics and physics, a tensor field is a function assigning a tensor to each point of a region of a mathematical space (typically a Euclidean space...

In mathematics, the signature (v, p, r)[clarification needed] of a metric tensor g (or equivalently, a real quadratic form thought of as a real symmetric...

It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures...

notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern...

differential geometry, the Einstein tensor (named after Albert Einstein; also known as the trace-reversed Ricci tensor) is used to express the curvature...

energy–momentum tensor and the Petrov classification of the Weyl tensor. There are various methods of classifying these tensors, some of which use tensor invariants...

^{*}M} of a Riemannian or pseudo-Riemannian manifold induced by its metric tensor. There are similar isomorphisms on symplectic manifolds. The term musical...

differential geometry, a tensor density or relative tensor is a generalization of the tensor field concept. A tensor density transforms as a tensor field when passing...

formula for the metric tensor g μ ν {\displaystyle g_{\mu \nu }\!} is called the Kerr–Newman metric. It is a generalisation of the Kerr metric for an uncharged...

{F} } . A (1,0) tensor is a vector. A (0,1) tensor is a covector. A (0,2) tensor is a bilinear form. An example is the metric tensor g μ ν . {\displaystyle...

In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature...

essentially the composition of functions. In the language of tensor algebra, a particular tensor is associated with a particular shape with many lines projecting...

relation exists in spaces not endowed with a metric tensor. Furthermore, from a more abstract standpoint, a tensor is simply "there" and its components of...