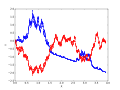
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution...

Stochastic partial differential equations (SPDEs) generalize partial differential equations via random force terms and coefficients, in the same way ordinary...

A backward stochastic differential equation (BSDE) is a stochastic differential equation with a terminal condition in which the solution is required to...

partial differential equations (PDEs) which may be with respect to more than one independent variable, and, less commonly, in contrast with stochastic differential...

In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions...

dynamical system and differential equation topics, by Wikipedia page. See also list of partial differential equation topics, list of equations. Deterministic...

In physics, a Langevin equation (named after Paul Langevin) is a stochastic differential equation describing how a system evolves when subjected to a combination...

Tsirelson's stochastic differential equation (also Tsirelson's drift or Tsirelson's equation) is a stochastic differential equation which has a weak solution...

with drift. It is an important example of stochastic processes satisfying a stochastic differential equation (SDE); in particular, it is used in mathematical...

In mathematics, stochastic analysis on manifolds or stochastic differential geometry is the study of stochastic analysis over smooth manifolds. It is...

stochastic processes such as Brownian motion (see Wiener process). It has important applications in mathematical finance and stochastic differential equations...

multifractals in turbulence, the stochastic differential equation for growth models for random aggregation (the Kardar–Parisi–Zhang equation) and his groundbreaking...

In mathematics, a partial differential equation (PDE) is an equation which computes a function between various partial derivatives of a multivariable function...

random variable Yt : Ω → Rn given by the solution to an Itō stochastic differential equation of the form d Y t = b ( t , Y t ) d t + σ ( t , Y t ) d B t...

can be generalized to stochastic systems, in which case the HJB equation is a second-order elliptic partial differential equation. A major drawback, however...

papers developing the field of stochastic calculus, which involves stochastic integrals and stochastic differential equations based on the Wiener or Brownian...

of assets—are stochastic. Backward stochastic differential equation Stochastic process Control theory Multiplier uncertainty Stochastic scheduling Definition...

convection–diffusion equation is a parabolic partial differential equation that combines the diffusion and convection (advection) equations. It describes physical...

stochastic differential equations (QSDE) that are analogous to classical Langevin equations. For the remainder of this article stochastic calculus will...

adjoint of the infinitesimal generator of the underlying stochastic process. The Klein–Kramers equation is a special case of that. For a Feller process ( X...

process x t {\displaystyle x_{t}} is defined by the following stochastic differential equation: d x t = − θ x t d t + σ d W t {\displaystyle dx_{t}=-\theta...

for ordinary differential equations are methods used to find numerical approximations to the solutions of ordinary differential equations (ODEs). Their...

of a stochastic differential equation (SDE). It is an extension of the Euler method for ordinary differential equations to stochastic differential equations...

backward stochastic differential equation method is a numerical method that combines deep learning with Backward stochastic differential equation (BSDE)...

particular, the theory of stochastic processes. He invented the concept of stochastic integral and stochastic differential equation, and is known as the founder...

differential equation Cauchy–Euler equation Riccati equation Hill differential equation Gauss–Codazzi equations Chandrasekhar's white dwarf equation Lane-Emden...

backward stochastic differential equation method is a numerical method that combines deep learning with Backward stochastic differential equation (BSDE)...

of a stochastic differential equation. It is named after Grigori N. Milstein who first published it in 1974. Consider the autonomous Itō stochastic differential...

backward stochastic differential equation method is a numerical method that combines deep learning with Backward stochastic differential equation (BSDE)...

case, the aforementioned controlled differential equation can be interpreted as a stochastic differential equation and integration against " d X t j {\displaystyle...