The Solovay–Strassen primality test, developed by Robert M. Solovay and Volker Strassen in 1977, is a probabilistic primality test to determine if a number...

prime. The Solovay–Strassen test is an Euler probable prime test (see PSW page 1003). For each individual value of a, the Solovay–Strassen test is weaker...

primality test and the Solovay–Strassen primality test. It is of historical significance in the search for a polynomial-time deterministic primality test. Its...

the Schönhage–Strassen algorithm. Strassen is also known for his 1977 work with Robert M. Solovay on the Solovay–Strassen primality test, the first method...

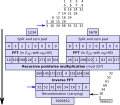
Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen in 1971...

continuum; Outside of set theory, developing (with Volker Strassen) the Solovay–Strassen primality test, used to identify large natural numbers that are prime...

test is not often used in the above form. Instead, other more powerful extensions of the Fermat test, such as Baillie–PSW, Miller–Rabin, and Solovay–Strassen...

complexity is O(p3). A more efficient multiplication algorithm is the Schönhage–Strassen algorithm, which is based on the Fast Fourier transform. It only requires...

The AKS primality test (also known as Agrawal–Kayal–Saxena primality test and cyclotomic AKS test) is a deterministic primality-proving algorithm created...

else return false end end end Probable prime Solovay, R.; Strassen, V. (1977-03-01). "A Fast Monte-Carlo Test for Primality". SIAM Journal on Computing....

Carlo algorithms include the Solovay–Strassen primality test, the Baillie–PSW primality test, the Miller–Rabin primality test, and certain fast variants...

Kanellakis Award for development of 'symbolic model checking,' used in testing computer system designs" (Press release). ACM. 26 Mar 1999. Archived from...

Strassen (1968). It was made practical and theoretical guarantees were provided in 1971 by Schönhage and Strassen resulting in the Schönhage–Strassen...

In computational number theory, the Lucas test is a primality test for a natural number n; it requires that the prime factors of n − 1 be already known...

mathematics, the Lucas–Lehmer–Riesel test is a primality test for numbers of the form N = k ⋅ 2n − 1 with odd k < 2n. The test was developed by Hans Riesel and...

(1963) is a faster generalization of Karatsuba's method, and the Schönhage–Strassen algorithm (1971) is even faster, for sufficiently large n. The standard...

primes (P = 1/2, Solovay–Strassen algorithm). Even when a deterministic primality proof is required, a useful first step is to test for probable primality...

primality test? (more unsolved problems in mathematics) The Baillie–PSW primality test is a probabilistic or possibly deterministic primality testing algorithm...

In computational number theory, the Adleman–Pomerance–Rumely primality test is an algorithm for determining whether a number is prime. Unlike other, more...

probabilistic Solovay–Strassen primality test and refinements such as the Baillie–PSW primality test and the Miller–Rabin primality test. As an indirect...

In mathematics, elliptic curve primality testing techniques, or elliptic curve primality proving (ECPP), are among the quickest and most widely used methods...

Pépin's test is a primality test, which can be used to determine whether a Fermat number is prime. It is a variant of Proth's test. The test is named...

efficiency results from the fact that, in binary representation, testing parity consists of testing the right-most digit, and dividing by two consists of removing...

discovered on 7 September 2013 by R. Propper. Increasing the number of curves tested improves the chances of finding a factor, but they are not linear with the...

achieved by extending the binary GCD algorithm using ideas from the Schönhage–Strassen algorithm for fast integer multiplication. The binary GCD algorithm has...

Pocklington–Lehmer primality test is a primality test devised by Henry Cabourn Pocklington and Derrick Henry Lehmer. The test uses a partial factorization...

is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples...

the empty product.) Testing whether the integer is prime can be done in polynomial time, for example, by the AKS primality test. If composite, however...

Miller, Rabin, Robert M. Solovay, and Volker Strassen were given the Paris Kanellakis Award for their work on primality testing. In 1976 he was invited...

Lucas–Lehmer Lucas–Lehmer–Riesel Proth's theorem Pépin's Quadratic Frobenius Solovay–Strassen Miller–Rabin Prime-generating Sieve of Atkin Sieve of Eratosthenes...