In number theory, Euler's theorem (also known as the Fermat–Euler theorem or Euler's totient theorem) states that, if n and a are coprime positive integers...

In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains...

In geometry, Euler's theorem states that the distance d between the circumcenter and incenter of a triangle is given by d 2 = R ( R − 2 r ) {\displaystyle...

naming everything after Euler, some discoveries and theorems are attributed to the first person to have proved them after Euler. Euler's conjecture (Waring's...

lower-case letter chi). The Euler characteristic was originally defined for polyhedra and used to prove various theorems about them, including the classification...

The Euclid–Euler theorem is a theorem in number theory that relates perfect numbers to Mersenne primes. It states that an even number is perfect if and...

Byrkit (1970, p. 80) See Euler's theorem. L. Euler "Theoremata arithmetica nova methodo demonstrata" (An arithmetic theorem proved by a new method), Novi...

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss...

little theorem are known. It is frequently proved as a corollary of Euler's theorem. Euler's theorem is a generalization of Fermat's little theorem: For...

mathematical field of differential geometry, Euler's theorem is a result on the curvature of curves on a surface. The theorem establishes the existence of principal...

Euler's identity (also known as Euler's equation) is the equality e i π + 1 = 0 {\displaystyle e^{i\pi }+1=0} where e {\displaystyle e} is Euler's number...

characteristic 0. The theorem was proven for two dimensions by Henri Poincaré and later generalized to higher dimensions by Heinz Hopf. The Euler characteristic...

and the Goldbach–Euler Theorem. He had a close friendship with famous mathematician Leonhard Euler, serving as inspiration for Euler's mathematical pursuits...

In mathematics, the Goldbach–Euler theorem (also known as Goldbach's theorem), states that the sum of 1/(p − 1) over the set of perfect powers p, excluding...

known as the Euler product formula for the Riemann zeta function. Euler proved Newton's identities, Fermat's little theorem, Fermat's theorem on sums of...

dynamics, the Euler equations are a set of partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular...

complex vector space can be considered as real vector spaces. Euler's homogeneous function theorem is a characterization of positively homogeneous differentiable...

Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric...

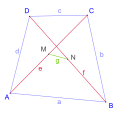
Euler's quadrilateral theorem or Euler's law on quadrilaterals, named after Leonhard Euler (1707–1783), describes a relation between the sides of a convex...

second factor zero, or they would not satisfy Fermat's little theorem. This is Euler's criterion. This proof only uses the fact that any congruence k...

posthumously in 1873 by Carl Hierholzer. This is known as Euler's Theorem: A connected graph has an Euler cycle if and only if every vertex has an even number...

theorem (geometry) Euler's rotation theorem (geometry) Euler's theorem (differential geometry) Euler's theorem (number theory) Euler's theorem in geometry (triangle...

In mathematics and computational science, the Euler method (also called the forward Euler method) is a first-order numerical procedure for solving ordinary...

geometry, the Gram–Euler theorem, Gram-Sommerville, Brianchon-Gram or Gram relation (named after Jørgen Pedersen Gram, Leonhard Euler, Duncan Sommerville...

millennia later, Leonhard Euler proved that all even perfect numbers are of this form. This is known as the Euclid–Euler theorem. It is not known whether...

sum of two primes, in a 1742 letter to Euler. Euler proved Alhazen's conjecture (now the Euclid–Euler theorem) that all even perfect numbers can be constructed...

still work out to ap − a, as needed.) This proof, due to Euler, uses induction to prove the theorem for all integers a ≥ 0. The base step, that 0p ≡ 0 (mod p)...

Chern theorem (or the Chern–Gauss–Bonnet theorem after Shiing-Shen Chern, Carl Friedrich Gauss, and Pierre Ossian Bonnet) states that the Euler–Poincaré...

the Euler characteristic of the 2-sphere is two. Therefore, there must be at least one zero. This is a consequence of the Poincaré–Hopf theorem. In the...

Adleman used Fermat's little theorem to explain why RSA works, it is common to find proofs that rely instead on Euler's theorem. We want to show that med...