Karl Theodor Wilhelm Weierstrass (/ˈvaɪərˌstrɑːs, -ˌʃtrɑːs/; German: Weierstraß [ˈvaɪɐʃtʁaːs]; 31 October 1815 – 19 February 1897) was a German mathematician...
16 KB (1,633 words) - 13:13, 21 October 2024
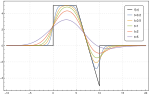
In mathematics, the Weierstrass function, named after its discoverer, Karl Weierstrass, is an example of a real-valued function that is continuous everywhere...
20 KB (2,395 words) - 13:55, 9 October 2024
original version of this result was established by Karl Weierstrass in 1885 using the Weierstrass transform. Marshall H. Stone considerably generalized...
27 KB (3,234 words) - 20:46, 8 June 2024
after Karl Weierstrass. These include: The Weierstrass approximation theorem, of which one well known generalization is the Stone–Weierstrass theorem...
1 KB (161 words) - 21:11, 28 February 2013
specifically in real analysis, the Bolzano–Weierstrass theorem, named after Bernard Bolzano and Karl Weierstrass, is a fundamental result about convergence...
12 KB (2,083 words) - 14:14, 24 August 2024
the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for Karl Weierstrass...
5 KB (934 words) - 14:37, 24 February 2024
complex numbers. It is named after the German mathematician Karl Weierstrass (1815-1897). Weierstrass M-test. Suppose that (fn) is a sequence of real- or complex-valued...
4 KB (711 words) - 18:35, 5 February 2024
mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class...
25 KB (4,401 words) - 20:49, 4 November 2024
linear factors, one for each root. The theorem, which is named for Karl Weierstrass, is closely related to a second result that every sequence tending...
10 KB (1,872 words) - 12:17, 9 April 2024
Extreme value theorem (redirect from Weierstrass extreme value theorem)
theorem is used to prove Rolle's theorem. In a formulation due to Karl Weierstrass, this theorem states that a continuous function from a non-empty compact...
22 KB (3,935 words) - 00:15, 17 November 2024
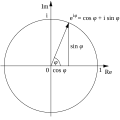
Tangent half-angle substitution (redirect from Weierstraß substitution)
{\textstyle t=-\cot(\psi /2).} Weierstrass, Karl (1915) [1875]. "8. Bestimmung des Integrals ...". Mathematische Werke von Karl Weierstrass (in German). Vol. 6....
21 KB (3,042 words) - 10:26, 12 August 2024
Wilhelm Killing (redirect from Wilhelm Karl Joseph Killing)
at the University of Münster and later wrote his dissertation under Karl Weierstrass and Ernst Kummer at Berlin in 1872. He taught in gymnasia (secondary...
10 KB (907 words) - 08:31, 4 November 2024
rational number. The theorem is named for Ferdinand von Lindemann and Karl Weierstrass. Lindemann proved in 1882 that eα is transcendental for every non-zero...
28 KB (4,778 words) - 23:00, 4 November 2024
mathematics, the Weierstrass transform of a function f : R → R {\displaystyle f:\mathbb {R} \to \mathbb {R} } , named after Karl Weierstrass, is a "smoothed"...
15 KB (2,866 words) - 14:52, 2 September 2024
and the concept of uniform convergence, and for being the teacher of Karl Weierstrass, who was greatly influenced by Gudermann's course on elliptic functions...
3 KB (225 words) - 20:05, 26 October 2024
named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass had previously described it in a paper written in 1841 but not published...
16 KB (2,776 words) - 05:15, 12 November 2024
Gamma function (redirect from Weierstrass definition of the gamma function)
the connection between the gamma function and elliptic integrals. Karl Weierstrass further established the role of the gamma function in complex analysis...
91 KB (13,517 words) - 14:35, 30 October 2024
received his Ph.D. in mathematics at Berlin, where he studied under Karl Weierstrass. In 1886, he became a professor at the Technische Hochschule Hannover...
7 KB (534 words) - 09:42, 20 August 2024
Kronecker, Kummer and Karl Weierstrass. He received his doctorate (awarded with distinction) in 1870 supervised by Weierstrass. His thesis was on the...
14 KB (1,445 words) - 19:10, 23 September 2024
Weierstrass is a small lunar impact crater that is attached to the northern rim of the walled plain Gilbert, in the eastern part of the Moon. It also...
5 KB (397 words) - 02:15, 26 January 2024
German mathematician Karl Weierstrass. Bolzano–Weierstrass theorem Casorati–Weierstrass theorem Weierstrass method Enneper–Weierstrass parameterization...
2 KB (107 words) - 18:08, 2 July 2024
German-born tightrope artist Karl Weierstrass (1815–1897), German mathematician Karl Wendlinger (born 1968), Austrian race car driver Karl Williams (born 1971)...
10 KB (1,212 words) - 03:45, 15 November 2024
Weber Werner Weber Katrin Wehrheim Dieter Weichert Joachim Weickert Karl Weierstrass Erhard Weigel Julius Weingarten Michael Weiss Paul Weiss Ernst August...
14 KB (1,105 words) - 06:05, 8 October 2024
Emma Levin (1868–1939) in 1896. He studied under Ernst Kummer and Karl Weierstrass, and was influenced by Felix Klein. The Schoenflies problem is to prove...
5 KB (370 words) - 07:40, 18 November 2024
the Casorati–Weierstrass theorem describes the behaviour of holomorphic functions near their essential singularities. It is named for Karl Theodor Wilhelm...
9 KB (1,256 words) - 13:40, 7 November 2024
century by the seminal work of Bernard Bolzano, Bernhard Riemann, and Karl Weierstrass, and on to the coining of the word fractal in the 20th century with...
75 KB (8,163 words) - 03:17, 14 November 2024
University of Berlin, where his supervisors were Ernst Kummer and Karl Weierstrass. He contributed to the solution of the prime number theorem by providing...
2 KB (131 words) - 19:23, 23 September 2024
gamma function. Karl Weierstrass called the reciprocal gamma function the "factorielle" and used it in his development of the Weierstrass factorization...
11 KB (1,437 words) - 14:18, 7 August 2024
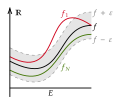
instances of faulty reasoning. The concept, which was first formalized by Karl Weierstrass, is important because several properties of the functions f n {\displaystyle...
30 KB (5,341 words) - 03:18, 21 October 2024
Durand–Kerner method (redirect from Weierstrass method)
In numerical analysis, the Weierstrass method or Durand–Kerner method, discovered by Karl Weierstrass in 1891 and rediscovered independently by Durand...
18 KB (3,079 words) - 20:04, 4 August 2024