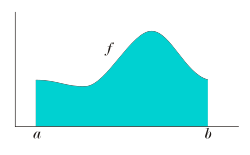
the Riemann–Stieltjes integral is a generalization of the Riemann integral, named after Bernhard Riemann and Thomas Joannes Stieltjes. The definition...

framework. The Lebesgue–Stieltjes integral is the ordinary Lebesgue integral with respect to a measure known as the Lebesgue–Stieltjes measure, which may be...

Thomas Stieltjes Institute for Mathematics at Leiden University, dissolved in 2011, was named after him, as is the Riemann–Stieltjes integral. Stieltjes was...

Henstock–Kurzweil integral or generalized Riemann integral or gauge integral – also known as the (narrow) Denjoy integral (pronounced [dɑ̃ʒwa]), Luzin integral or Perron...

Lebesgue–Stieltjes integral, further developed by Johann Radon, which generalizes both the Riemann–Stieltjes and Lebesgue integrals. The Daniell integral, which...

The Laplace–Stieltjes transform, named for Pierre-Simon Laplace and Thomas Joannes Stieltjes, is an integral transform similar to the Laplace transform...

central concept is the Itô stochastic integral, a stochastic generalization of the Riemann–Stieltjes integral in analysis. The integrands and the integrators...

products. The Lebesgue–Stieltjes integral is the ordinary Lebesgue integral with respect to a measure known as the Lebesgue–Stieltjes measure, which may be...

Riemann–Stieltjes integral, and most disappear with the Lebesgue integral, though the latter does not have a satisfactory treatment of improper integrals. The...

Riemann–Stieltjes integral, along with an appropriate function of bounded variation, gives a definition of integral equivalent to the Lebesgue–Stieltjes integral...

: 13–15  Other integrals can be approximated by versions of the Gaussian integral. Fourier integrals are also considered. The first integral, with broad...

Measure Sigma-algebra Lebesgue space Lebesgue–Stieltjes integration Riemann integral Henstock–Kurzweil integral This approach can be found in most treatments...

f^{-1}} is not differentiable: it suffices, for example, to use the Stieltjes integral in the previous argument. On the other hand, even though general monotonic...

Kolmogorov integral (or Kolmogoroff integral) is a generalized integral introduced by Kolmogoroff (1930) including the Lebesgue–Stieltjes integral, the Burkill...

Length Area Volume Probability Moving average Riemann sum Riemann–Stieltjes integral Bounded variation Jordan content Cauchy principal value Measure (mathematics)...

Partitions are used in the theory of the Riemann integral, the Riemann–Stieltjes integral and the regulated integral. Specifically, as finer partitions of a given...

variation are precisely those with respect to which one may find Riemann–Stieltjes integrals of all continuous functions. Another characterization states that...

FX of X, with the expected value of g(X) now given by the Lebesgue–Stieltjes integral E ⁡ [ g ( X ) ] = ∫ − ∞ ∞ g ( x ) d F X ( x ) . {\displaystyle \operatorname...

style of a Riemann–Stieltjes integral). Many integration techniques of ordinary calculus can be used for the Stratonovich integral, e.g.: if f : R → R...

integrator in a Stieltjes integral is represented as the differential of a function. Formally, the differential appearing under the integral behaves exactly...

integral in his habilitation. Among other things, he showed that every piecewise continuous function is integrable. Similarly, the Stieltjes integral...

topics such as continuous functions, differentiation, the Riemann–Stieltjes integral, sequences and series of functions (in particular uniform convergence)...

corresponding Lebesgue–Stieltjes measure, and the integral with respect to the Lebesgue–Stieltjes measure agrees with the Riemann–Stieltjes integral for continuous...

against a continuous function can be properly understood as a Riemann–Stieltjes integral: ∫ − ∞ ∞ f ( x ) δ ( d x ) = ∫ − ∞ ∞ f ( x ) d H ( x ) . {\displaystyle...

formulations of integration by parts exist for the Riemann–Stieltjes and Lebesgue–Stieltjes integrals. The discrete analogue for sequences is called summation...

integration and measure theory topics Riemann integral, Riemann sum Riemann–Stieltjes integral Darboux integral Lebesgue integration Monotone convergence...

bounded on the interval (0, A] for some 0 ≤ α < 1. The q-integral is a Riemann–Stieltjes integral with respect to a step function having infinitely many...

the Riemann–Stieltjes integral, and where F {\displaystyle F} is the cumulative distribution function. This is simply the Laplace-Stieltjes transform of...

_{-\infty }^{\infty }e^{2\pi i\tau f}dF(f),} where the integral is a Riemann–Stieltjes integral. The asterisk denotes complex conjugate, and can be omitted...

}{2}}.} The (unilateral) Laplace–Stieltjes transform of a function g : ℝ → ℝ is defined by the Lebesgue–Stieltjes integral { L ∗ g } ( s ) = ∫ 0 ∞ e − s...