} This norm is also called the supremum norm, the Chebyshev norm, the infinity norm, or, when the supremum is in fact the maximum, the max norm. The name...
8 KB (1,269 words) - 06:57, 27 December 2024
denotes the supremum. This norm measures how much the mapping induced by A {\displaystyle A} can stretch vectors. Depending on the vector norms ‖ ⋅ ‖ α {\displaystyle...
28 KB (4,788 words) - 21:25, 24 May 2025
Haar measure). These norms are also valid in the limit as p → + ∞ {\displaystyle p\rightarrow +\infty } , giving a supremum norm, and are called ℓ ∞ {\displaystyle...
36 KB (5,937 words) - 20:03, 19 June 2025
complete metric space, with respect to the supremum norm. However, the supremum norm does not give a norm on the space C(a, b) of continuous functions...
16 KB (2,509 words) - 21:18, 28 April 2025
exists. If the supremum of S {\displaystyle S} exists, it is unique, and if b is an upper bound of S {\displaystyle S} , then the supremum of S {\displaystyle...
25 KB (4,523 words) - 14:12, 31 December 2024
Banach space (redirect from Banach norm)
}\|_{\infty })} denote the Banach space of continuous functions with the supremum norm and let τ ∞ {\displaystyle \tau _{\infty }} denote the topology on C...
102 KB (17,049 words) - 16:58, 14 April 2025
operator norm measures the "size" of certain linear operators by assigning each a real number called its operator norm. Formally, it is a norm defined...
15 KB (2,557 words) - 13:48, 22 April 2025
L^{\infty }} consisting of bounded functions on the real line with the supremum norm, then the map φ {\displaystyle \varphi } is not surjective. (See L p...
22 KB (2,943 words) - 14:45, 18 February 2025
for all x in [a, b], we have |f(x) − p(x)| < ε, or equivalently, the supremum norm ‖f − p‖ < ε. A constructive proof of this theorem using Bernstein polynomials...
27 KB (3,235 words) - 20:19, 2 June 2025
Banach algebra (redirect from Algebra norm)
functions defined on some set (with pointwise multiplication and the supremum norm) is a unital Banach algebra. The algebra of all bounded continuous real-...
17 KB (2,618 words) - 09:10, 24 May 2025
{\displaystyle \ell ^{\infty }} of all bounded real sequences, with the supremum norm, is not separable. The same holds for L ∞ {\displaystyle L^{\infty }}...
15 KB (2,090 words) - 10:21, 10 February 2025
L-infinity (category Normed spaces)
, the (real or complex) vector space of bounded sequences with the supremum norm, and L ∞ = L ∞ ( X , Σ , μ ) {\displaystyle L^{\infty }=L^{\infty }(X...
5 KB (770 words) - 20:18, 23 March 2025
0 {\displaystyle c_{0}} the space of convergent sequences with the supremum norm has the AK property. ℓ p {\displaystyle \ell ^{p}} ( 1 ≤ p < ∞ {\displaystyle...
1 KB (200 words) - 11:37, 9 April 2025
φn : [0, T] → X converging uniformly to f (i.e. with respect to the supremum norm || - ||∞). It requires a little work to show that these two conditions...
8 KB (1,024 words) - 13:48, 6 September 2020
Total variation (redirect from Total variation norm)
{\displaystyle \Vert \;\Vert _{L^{\infty }(\Omega )}} is the essential supremum norm, and div {\displaystyle \operatorname {div} } is the divergence operator...
25 KB (3,547 words) - 10:19, 19 June 2025
linear maps are called "functionals". The norm of a functional φ {\displaystyle \varphi } is defined as the supremum of | φ ( v ) | {\displaystyle |\varphi...
18 KB (2,881 words) - 18:43, 8 May 2025
Dual space (redirect from Norm dual)
the Banach spaces c (consisting of all convergent sequences, with the supremum norm) and c0 (the sequences converging to zero) are both naturally identified...
45 KB (6,865 words) - 10:32, 17 March 2025
Mathematically, the Chebyshev distance is a metric induced by the supremum norm or uniform norm. It is an example of an injective metric. In two dimensions...
7 KB (828 words) - 09:58, 13 April 2025
of weighted Hölder norms; the notation will follow that given in the text of D. Gilbarg and Neil Trudinger (1983). The supremum norm of a continuous function...
9 KB (1,570 words) - 00:24, 25 May 2025
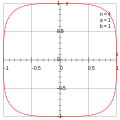
Squircle (section p-norm notation)
square is given by the p → ∞ case (the supremum norm), and a rotated square is given by p = 1 (the taxicab norm). This allows a straightforward generalization...
14 KB (1,991 words) - 22:21, 25 June 2025
{\displaystyle \ell ^{\infty }} with respect to the supremum norm, and so it is a Banach space with respect to this norm. A sequence that converges to 0 {\displaystyle...
22 KB (3,611 words) - 04:41, 14 June 2025
of bounded sequences ℓ ∞ {\displaystyle \ell ^{\infty }} under the supremum norm ‖ ⋅ ‖ ∞ . {\displaystyle \|\cdot \|_{\infty }.} The space of absolutely...
1 KB (158 words) - 12:41, 18 June 2024
Function space (section Uniform norm)
{\text{where}}\ \ y\in {\mathcal {C}}(a,b)} is called the uniform norm or supremum norm ('sup norm'). Kolmogorov, A. N., & Fomin, S. V. (1967). Elements of the...
9 KB (1,225 words) - 11:21, 22 June 2025
equations with local monotonicity and coercivity assumption with respect to supremum norm. Let X ( t ) , t ≥ 0 {\displaystyle X(t),\,t\geq 0} be a non-negative...
3 KB (593 words) - 20:57, 22 June 2025
concepts of essential infimum and essential supremum are related to the notions of infimum and supremum, but adapted to measure theory and functional...
9 KB (1,764 words) - 17:54, 18 April 2025
{\displaystyle A_{\infty }(\Omega )} of all bounded analytic functions with the supremum norm is a Banach space. A polynomial cannot be zero at too many points unless...
16 KB (2,233 words) - 23:44, 25 May 2025
of continuous functions under the L ∞ {\displaystyle L^{\infty }} (supremum) norm. The conventions chosen in this article are those of harmonic analysis...
177 KB (21,313 words) - 02:40, 6 July 2025
on the interval [ a , b ] , {\displaystyle [a,b],} equipped with the supremum norm. Every metric space is dense in its completion. Every topological space...
12 KB (1,911 words) - 13:33, 2 May 2024
R {\textstyle [0,1]\to \mathbb {R} } . It is a function space with supremum norm (it is a Banach space). Let f {\textstyle f} be a continuous function...
26 KB (3,986 words) - 10:52, 28 June 2025