of its namesake the Möbius inversion formula. Following work of Gian-Carlo Rota in the 1960s, generalizations of the Möbius function were introduced into...
22 KB (3,124 words) - 07:23, 26 June 2025
Ferdinand Möbius. A large generalization of this formula applies to summation over an arbitrary locally finite partially ordered set, with Möbius' classical...
16 KB (2,762 words) - 05:29, 19 June 2025
Leipzig. Möbius died in Leipzig in 1868 at the age of 77. His son Theodor was a noted philologist. He is best known for his discovery of the Möbius strip...
8 KB (682 words) - 01:05, 16 June 2025
Incidence algebra (redirect from Generalized Möbius function)
the zeta function is the Möbius function μ(a, b); every value of μ(a, b) is an integral multiple of 1 in the base ring. The Möbius function can also be...
18 KB (3,019 words) - 12:52, 20 June 2025
_{k=1}^{n}\mu (k),} where μ ( k ) {\displaystyle \mu (k)} is the Möbius function. The function is named in honour of Franz Mertens. This definition can be...
16 KB (2,328 words) - 00:05, 20 June 2025
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form f ( z ) = a z + b c z + d {\displaystyle...
70 KB (10,603 words) - 19:06, 8 June 2025
{n}{d}}=n\sum _{d\mid n}{\frac {\mu (d)}{d}},} where μ is the Möbius function, the multiplicative function defined by μ ( p ) = − 1 {\displaystyle \mu (p)=-1} and...
44 KB (6,519 words) - 13:19, 27 June 2025
has no prime factors, Ω(1) = 0, so λ(1) = 1. It is related to the Möbius function μ(n). Write n as n = a2b, where b is squarefree, i.e., ω(b) = Ω(b)...
11 KB (1,812 words) - 12:43, 30 May 2025
Permutation pattern (section Möbius function)
its Möbius function, a goal first explicitly presented by Wilf (2002). The goal in such investigations is to find a formula for the Möbius function of...
31 KB (3,647 words) - 05:11, 25 June 2025
the Riemann zeta function. The generating function of the Möbius function is the inverse of the zeta function: ζ ( s ) ∑ n = 1 ∞ μ ( n ) n s = 1 , ℜ s...
53 KB (7,555 words) - 01:12, 6 April 2025
\left(x^{1/n}\right),} μ(n) is the Möbius function, li(x) is the logarithmic integral function, ρ indexes every zero of the Riemann zeta function, and li(xρ/n) is not...
36 KB (4,660 words) - 20:32, 8 April 2025
indicator function may be defined. This is commonly called the generalized Möbius function, as a generalization of the inverse of the indicator function in elementary...
17 KB (2,543 words) - 13:47, 8 May 2025
Dirichlet convolution (category Arithmetic functions)
=\varepsilon } , the Dirichlet inverse of the constant function 1 {\displaystyle 1} is the Möbius function (see proof). Hence: g = f ∗ 1 {\displaystyle g=f*1}...
16 KB (2,587 words) - 06:05, 30 April 2025
bigger than) n {\displaystyle n} μ ( n ) {\displaystyle \mu (n)} : the Möbius function, the parity ( − 1 {\displaystyle -1} for odd, + 1 {\displaystyle +1}...
19 KB (3,626 words) - 10:16, 30 June 2025
zeta series. The reciprocal of the zeta function may be expressed as a Dirichlet series over the Möbius function μ(n): 1 ζ ( s ) = ∑ n = 1 ∞ μ ( n ) n s...
74 KB (10,718 words) - 01:21, 7 July 2025
constants. The function ω ( n ) {\displaystyle \omega (n)} is related to divisor sums over the Möbius function and the divisor function, including: ∑ d...
20 KB (4,100 words) - 06:12, 26 May 2025
Riemann hypothesis (category Zeta and L-functions)
of many other arithmetic functions, in addition to the primes counting function above. One example involves the Möbius function μ. The statement that the...
127 KB (16,781 words) - 22:34, 19 June 2025
Nilsequence (section Möbius function and nilsequences)
involving only the Möbius function, and the way it self-correlates. Peter Sarnak made a conjecture on the non-correlation of the Möbius function with more general...
10 KB (1,265 words) - 09:48, 9 February 2025
differential equations the degree of membership in a fuzzy set the Möbius function in number theory the population mean or expected value in probability...
14 KB (1,677 words) - 20:33, 16 June 2025
z)=\sum \limits _{d\mid P(z)}\mu (d)A_{d}(x)} by using the Möbius function and some functions A d ( x ) {\displaystyle A_{d}(x)} induced by the elements...
15 KB (2,521 words) - 21:10, 20 December 2024
\mu } denotes the Möbius function and k {\displaystyle k} denotes a positive integer, generalize the von Mangoldt function. The function Λ 1 {\displaystyle...
11 KB (1,839 words) - 02:56, 24 March 2024
− 1 ) 2 x = 1 {\displaystyle \mu (n)=(-1)^{2x}=1} (where μ is the Möbius function and x is half the total of prime factors), while for the former μ (...
6 KB (851 words) - 18:31, 9 July 2025
the difference (XOR) of the function at x and x + dx. The Möbius transform (or Boole–Möbius transform) of a Boolean function is the set of coefficients...
23 KB (2,887 words) - 21:32, 19 June 2025
\mu \cdot f} where μ {\displaystyle \mu } is the Möbius function. Completely multiplicative functions also satisfy a distributive law. If f is completely...
6 KB (1,008 words) - 09:43, 9 August 2024
{\displaystyle \mu (n)} , which generally denotes the Möbius function). Möbius inversion formula Heaviside step function Kronecker delta Estrada, Ricardo (1995), "Dirichlet...
1 KB (141 words) - 00:48, 20 April 2025
|\,n}\mu \left({n \over d}\right)\alpha ^{d},} and μ is the classic Möbius function of number theory. The name comes from the denominator, 1 − z j, which...
2 KB (283 words) - 11:23, 25 December 2020
Möbius μ function: Sum of the nth primitive roots of unity, it depends on the prime factorization of n. Prime omega functions Chebyshev functions Liouville...
10 KB (1,065 words) - 15:31, 16 June 2025
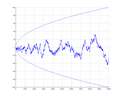
Mertens function is defined as M ( n ) = ∑ 1 ≤ k ≤ n μ ( k ) , {\displaystyle M(n)=\sum _{1\leq k\leq n}\mu (k),} where μ(k) is the Möbius function; the...
11 KB (1,442 words) - 15:10, 16 January 2025
)}} , and thus this poset is Eulerian, meaning its Möbius function is produced by the rank function on the poset. Kazhdan–Lusztig polynomial Chevalley...
5 KB (656 words) - 03:53, 28 May 2025