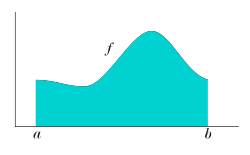
d\mu .} The function is Lebesgue integrable if and only if its absolute value is Lebesgue integrable (see Absolutely integrable function). Consider the...

condition than Lebesgue-integrability. The converse does not hold; not all Lebesgue-integrable functions are Riemann integrable. The Lebesgue–Vitali theorem does...

related branches of mathematics, Lebesgue–Stieltjes integration generalizes both Riemann–Stieltjes and Lebesgue integration, preserving the many advantages...

theorem. Remark 4. While f {\displaystyle f} is Lebesgue integrable, it is not in general Riemann integrable. For example, order the rationals in [ 0 , 1...

coefficient tends to zero (the Riemann–Lebesgue lemma), and that a Fourier series is integrable term by term. In 1904-1905 Lebesgue lectured once again at the Collège...

mathematics, Lebesgue integrability may refer to: Whether the Lebesgue integral of a function is defined; this is what is most often meant. The Lebesgue integrability...

functions are Lebesgue-integrable. Integrals may be generalized depending on the type of the function as well as the domain over which the integration is performed...

\int _{a}^{b}g(x)\,dx.} If f is Riemann or Lebesgue integrable, then it is also Henstock–Kurzweil integrable, and calculating that integral gives the same...

In mathematics, a square-integrable function, also called a quadratically integrable function or L 2 {\displaystyle L^{2}} function or square-summable...

by Guido Fubini in 1907. The theorem states that if a function is Lebesgue integrable on a rectangle X × Y {\displaystyle X\times Y} , then one can evaluate...

be differentiable almost everywhere and its derivative f ′ may be Lebesgue integrable, but the integral of f ′ differs from the increment of f (how much...

II of the theorem is true for any Lebesgue integrable function f, which has an antiderivative F (not all integrable functions do, though). In other words...

particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set...

mathematics, the Lebesgue differentiation theorem is a theorem of real analysis, which states that for almost every point, the value of an integrable function...

not be integrable. For example, the Fourier transform of the rectangular function, which is integrable, is the sinc function, which is not Lebesgue integrable...

improper integration is not necessary, and this is seen as a strength of the theory: it encompasses all Lebesgue integrable and improper Riemann integrable functions...

{\displaystyle a<b} , so the Dirichlet function is not Darboux-integrable (and therefore not Riemann-integrable) over any nondegenerate interval. The Dirichlet function...

In mathematics, an absolutely integrable function is a function whose absolute value is integrable, meaning that the integral of the absolute value over...

Integration by parts works if u {\displaystyle u} is absolutely continuous and the function designated v ′ {\displaystyle v'} is Lebesgue integrable (but...

function w on X such that for every Lebesgue integrable function f : Y → R, the function (f ∘ φ) ⋅ w is Lebesgue integrable on X, and ∫ Y f ( y ) d ρ ( y )...

In mathematics, given a locally Lebesgue integrable function f {\displaystyle f} on R k {\displaystyle \mathbb {R} ^{k}} , a point x {\displaystyle x}...

x}{x}}\right|} has an infinite Lebesgue or Riemann improper integral over the positive real line, so the sinc function is not Lebesgue integrable over the positive...

Riemann-integrable functions on compact sets. Riemann-integrable functions are better-behaved than Lebesgue-integrable functions. Lebesgue-integrable functions...

that fx(x,t) is Lebesgue integrable, but not that it is Riemann integrable. In the former (stronger) proof, if f(x,t) is Riemann integrable, then so is fx(x...

functions defined on a measure space (S,Σ,μ). If there exists a Lebesgue-integrable function g on S which dominates the sequence in absolute value, meaning...

Integrability may refer to: Bronshtein-integrability (informal) Frobenius integrability Riemann-integrability Lebesgue-integrability; see Lebesgue integral...

equivalent, in the sense that a function is Darboux integrable if and only if it is Riemann integrable, and the values of the integrals are equal. In fact...

Pettis integrable if and only if each of f {\displaystyle f} ’s coordinates is Lebesgue integrable. If f {\displaystyle f} is Pettis integrable and A ∈...

stochastic integration implies that H is X-integrable, with integral H · X = Y, if and only if Y0 = 0 and K · Y = (KH) · X. The set of X-integrable processes...

defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected...