تمدد الزمن الثقالي - ويكيبيديا
تمدد الزمن الثقالي (بفعل الجاذبية) هو شكل من أشكال تمدد الزمن، حيث يتمدد الزمن ويحدث فرق فعلي في الزمن الفاصل بين حدثين عندما يتم قياس هذا الزمن بواسطة مراقبين يرون الحدث من مسافات مختلفة عن الكتلة ذات الجاذبية. كلما قلت المسافة عن مصدر الجاذبية (كلما كانت الساعة أقرب إلى مصدر الجاذبية) زاد بطء مرور الزمن، كلما ابتعدت الساعة عن مصدر الجاذبية زادت سرعة مرور الزمن. ألبرت أينشتاين كان أول من توقع هذا التأثير في نظريته عن النسبية وتم إثبات ذلك من ذلك الحين عبر تجارب النسبية العامة.[1]
أُثبت ذلك عن طريق ملاحظة أن الساعات الذرية عند وضعها على ارتفاعات مختلفة، بالتالي جاذبية مختلفة، ستبدأ كل ساعة منها بإظهار زمن مختلف عن الأخرى. الاختلافات الحاصلة في التجارب التي تحصل على الأرض صغيرة جداً، حيث تقاس الاختلافات في قياس الزمن بالنانوثانية.
باتباع الفكرة ذاتها، بالنسبة لعمر الأرض الذي يبلغ مليارات السنين، عمر أعماق الأرض أقل بسنتين ونصف من سطحها.[2]
لكي نرى آثار أكبر من ذلك فإن الأمر يتطلب أن نبتعد مسافات أبعد عن الأرض، أو عن أي جرم سماوي ذا جاذبية عالية.
ألبرت آينشتاين كان أول من ذكر مفهوم تمدد الزمن بفعل الجاذبية في عام 1907 كنتيجة لتطبيق نظرية النسبية الخاصة على الأطر المرجعية المتسارعة (الأجسام السماوية التي تتسارع حركتها ولا يمكن قياس سرعتها). تم تأكيد وجود تمدد زمني بفعل الجاذبية لأول مرة مباشرة من خلال تجربة Pound-Rebka في عام 1959.
تعريف
[عدل]الساعات التي توضع بعيداً عن الأجرام الضخمة (في مجال جاذبي واسع) تجري بشكل أسرع، بينما الساعات التي تقع على مقربة من الأجرام الضخمة تسير بشكل أبطأ. على سبيل المثال: باعتبار عمر الأرض (4.6 بليون سنة) ستكون ساعة موضوعة بشكل ثابت على ارتفاع 9000 متر من سطح البحر متقدمة بـ 39 ساعة عن ساعة أخرى موضوعة على سطح موازي لسطح البحر. هذا لأن تمدد الزمن الثقالي يتضح في الأطر المرجعية المتسارعة، بفضل مبدأ التكافؤ في مجال جاذبية الأجرام السماوية الضخمة.
خصائص مهمة لتمدد الزمن بفعل الجاذبية
[عدل]- بحسب نظرية النسبية العامة، تمدد الزمن بفعل الجاذبية مرتبط بوجود إطار مرجعي متسارع. بالإضافة لذلك، فإن كل الظواهر الملموسة اللي تتعرض لظروف متشابهة تواجه تمدد زمن بفعل الجاذبية بالمقدار نفسه، وذلك بحسب مبدأ التكافؤ في نظرية النسبية العامة.
- سرعة الضوء في أي مكان تساوي c من منظور المراقب الموجود في هذا المكان. بمعنى أن لكل منطقة متناهية الصغر في الزمكان وقتها الخاص، لكن سرعة الضوء في ذلك المكان ستكون دائماً c. وستكون دائماً كذلك سواءً كان هنالك مراقب أم لم يكن.
- يوجد هنالك تمدد زمني من الممكن قياسه للفوتونات الصادرة عن الأرض، التي تنثني حول الشمس، ثم تسافر إلى الزهرة، ثم تعود إلى الأرض في نفس المسار.
- في هذا المثال، لا يوجد إخلال بثبات سرعة الضوء، كل مراقب يراقب سرعة الفوتونات في منطقته سيرى أن سرعتها هي c، لكن الضوء الناتج عن المراقب ستكون سرعته أثناء انتقاله حول الشمس مختلفةً عن c.
التجارب المثبتة
[عدل]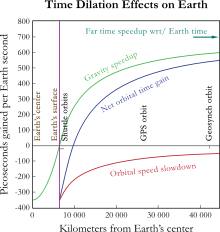
تم قياس التمدد الزمني بفعل الجاذبية بتجارب استعملت فيها ساعات ذرية على متن طائرات.
الساعات اللآتي على الطائرات أسرع قليلاً من الساعات على سطح الأرض. هذا الأمر له تأثير كافي لكي يجعل أنظمة الملاحة عبر الأقمار الصناعية GPS تحتاج لتصحح القراءة التي تصدرها ساعاتها في الأقمار الصناعية لتتفق مع الساعات على سطح الأرض.[3]
كما أنه تم -مختبرياً- إثبات تمدد الزمن الحاصل عن اختلاف ارتفاع الساعات حتى في مسافة تقل عن 1 متر.[4]
انظر أيضاً
[عدل]المراجع
[عدل]- ^ Albert (01/02/2004). Relativity : the Special and General Theory. Methuen & Co Ltd, 1920. مؤرشف من الأصل في 2019-08-21.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ=(مساعدة)صيانة الاستشهاد: مكان (link) - ^ Uggerhoj، Ulrik I.؛ Mikkelsen، Rune E.؛ Faye، Jan (1 مايو 2016). "The young centre of the Earth". European Journal of Physics. ج. 37 ع. 3: 035602. DOI:10.1088/0143-0807/37/3/035602. ISSN:0143-0807. مؤرشف من الأصل في 2020-01-11.
- ^ Richard (2003). Simply Einstein: Relativity Demystified (بالإنجليزية). W. W. Norton & Company. ISBN:978-0-393-05154-4. Archived from the original on 2020-02-28.
- ^ Chou, C. W.; Hume, D. B.; Rosenband, T.; Wineland, D. J. (24 Sep 2010). "Optical Clocks and Relativity". Science (بالإنجليزية). 329 (5999): 1630–1633. DOI:10.1126/science.1192720. ISSN:0036-8075. PMID:20929843. Archived from the original on 2019-10-17.


 French
French Deutsch
Deutsch