دالة متباينة - ويكيبيديا

في الرياضيات، الدالة المتباينة (بالإنجليزية: Injective function)‏ هي دالة تبقى بها العناصر متباينة (متفاوتة): فبها لا تقترن العناصر المتباينية من مجالها بنفس العنصر من مجالها المقابل. بمعنى أن كل عنصر من مجالها المقابل مقترن بعنصر من مجالها واحد على الأكثر.

تعريف

لتكن f دالة مجال تعريفها هو مجموعة A. الدالة f هي متباينة إذا وفقط إذا توفر لكل عنصرين a و b من A ما يلي:

إذا كان (f(a) = f(b، فإن a = b؛ أي أن (f(a) = f(b تعني a = b. وبشكل مكافئ، إذا كان a ≠ b، فإن (f(a) ≠ f(b.

باستعمال رموز الرياضيات، يُحصل على ما يلي:

\forall a,b\in A,\;\;f(a)=f(b)\Rightarrow a=b

والتي تكافئ بشكل منطقي ما يلي:

\forall a,b\in A,\;\;a\neq b\Rightarrow f(a)\neq f(b)

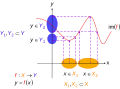
دوال متباينة. تفسير هندسي في نظام إحداثي ديكارتي, المعرفة بالتطبيق f : X → Y, حيث y = f(x), X = مجال دالة, Y = مدى دالة, و im(f) يرمز إلى صورة of f. Every one x في X maps to exactly one unique y in Y. الأجزاء المدورة من المحورين تمثل domain و range sets – في توافق مع المخططات المستعملة في التعريف أعلاه.
دالة غير متباينة. في هذه الحالة X₁ و X₂ هما مجموعتان جزئيتان من X, Y₁ و Y₂ are مجموعتان جزئيتان من Y: for two regions حيث الدالة غير متباينة لأن more than one domain عنصر can map to a single range element. That is, it is possible for more than one x في X to map to the same y في Y
Making functions injective. الدالة السابقة f : X → Y can be reduced to one or more injective functions (say) f : X₁ → Y₁ و f : X₂ → Y₂, shown by solid curves (long-dash parts of initial curve are not mapped to anymore). Notice how the rule f has not changed – only the domain و range. X₁ و X₂ are مجموعتان جزئيتان من X, Y₁ و Y₂ هما مجموعتان جزئيتان من R: for two regions حيث الدالة الأولى can be made متباينة so that one domain element can map to a single range element. هكذا, only one x في X maps to one y في Y.