Координатна система – Уикипедия

Координатната система е система в геометрията, която използва числа, наричани координати, за да определи еднозначно положението на точките или на други геометрични обекти в дадено пространство или по-общо – в дадено математическо многообразие.^[1][2] Координатите на дадена точка могат да бъдат различни геометрични величини, като обикновено те са разстояния от точката до определен обект или ъгли между радиус-вектора на точката и определен обект.

Подредбата на координатите има свое значение, като понякога те се идентифицират чрез положението си в наредена група, а в други случаи с определено буквено означение, например „x-координата“. Броят на координатите съответства на размерността на съответното пространство – дадена координатна система може да определя положението на точки върху права (1 координата), равнина (2 координати), триизмерно евклидово пространство (3 координати), фазово пространство в механиката (6 координати) и т.н. Координатите най-често са реални числа, но могат да бъдат и комплексни числа или елементи на по-абстрактни системи, като комутативни пръстени.

Използването на координатни системи дават възможност геометрични задачи да се преобразуват в числови и обратното, като по този начин те са в основата на аналитичната геометрия.^[3]

 Основна статия: Числова ос

Най-простият пример за координатна система е определянето на точките от дадена права чрез реалните числа чрез използване на числова ос. При нея се избира произволна точка O (начална точка), лежаща на правата. Координатата на всяка точка P от правата се дефинира като разстоянието от точка O до точка P, взето с положителен или отрицателен знак, в зависимост от това от коя страна на началната точка е разположена точката P. По този начин всяка точка има една единствена координата и всяко реално число е координатата на една единствена точка.^[4]

 Основна статия: Декартова координатна система

Исторически най-рано създадената (през XVII век от френския математик Рене Декарт, чието име носи) и най-широко използваната в практиката координатна система е декартовата, наричана също правоъгълна.

В равнината декартовата координатна система използва две перпендикулярни прави, като координатите на дадена точка са разстоянията до всяка от тях, взети с положителен или отрицателен знак, в зависимост от това, от коя страна на правата е разположена точката. В триизмерното пространство координатната система използва три взаимно перпендикулярни равнини и координатите на дадена точка са разстоянията до всяка от тях, отново взети със съответния знак.^[5] Същият принцип може да бъде приложен и към пространства с повече от три измерения.

В двуизмерното и триизмерното пространство координатите на декартовата (и афинната – вижте по-долу) координатна система имат следните наименования:

• Абсциса – първата координата на една точка. Стандартното означение на абсцисата е x. В координатна система оста, по която се измерва абсцисата, се нарича абсцисна ос и се означава с ${\displaystyle {\vec {x}}}$.
• Ордината – втората координата на една точка. Стандартното означение на ординатата е y. В координатна система оста, по която се измерва ординатата, се нарича ординатната ос и се означава с ${\displaystyle {\vec {y}}}$.
• Апликата – третата координата на една точка. Стандартното означение на апликатата е z. В координатна система оста, по която се измерва апликатата, се нарича респективно апликатна ос и се означава със ${\displaystyle {\vec {z}}}$.

В зависимост от взаимното положение на положителните посоки на осите, координатните системи могат да бъдат десни или леви.

От гледна точка на аналитичната геометрия декартовата координатна система може да се разглежда като множеството от произволна точка O и базис от n взаимно перпендикулярни единични вектора (${\displaystyle {\vec {e_{1}}},{\vec {e_{2}}},...,{\vec {e_{n}}}}$) с начало в O, където n е размерността на пространството на координатната система. Точката O е началото на координатната система, а правите ${\displaystyle Oe_{i}}$ са нейни координатни оси.

Така радиус-векторът ${\displaystyle {\vec {OM}}}$ на произволна точка M от пространството на системата може да бъде представен като линейна комбинация на векторите ${\displaystyle {\vec {e_{i}}}}$:

${\displaystyle {\vec {OM}}=\sum _{i=1}^{n}x_{i}{\vec {e_{i}}}}$

Това равенство задава взаимно еднозначно съответствие на множеството от точките M върху множеството на наредените n-орки ${\displaystyle (x_{1},x_{2},...,x_{n})}$. Още се казва, че M има координати ${\displaystyle (x_{1},x_{2},...,x_{n})}$ спрямо системата ${\displaystyle O{e_{1}}{e_{2}}...{e_{n}}}$ и се бележи с ${\displaystyle M(x_{1},x_{2},...,x_{n})}$.

Координатите ${\displaystyle x_{i}}$ са алгебрични проекции на вектора ${\displaystyle {\vec {OM}}}$ върху координатните оси, измерени със съответния с координатен вектор ${\displaystyle {\vec {e_{i}}}}$.

 Основна статия: Афинна координатна система

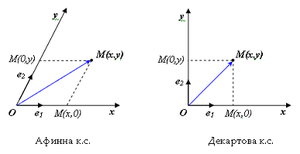
Декартовата координатна система е частен случай на афинна координатна система – тя използва базис, който е ортонормиран – съставен е от взаимно перпендикулярни единични вектори. Множеството от всички точки в пространството може да бъде описано и като линейна комбинация на вектори, които не са единични и не са взаимно перпендикулярни – достатъчно условие е те да бъдат линейно независими. Афинните координатни системи използват такъв произволен базис.

 Основна статия: Полярна координатна система

Друга често използвана координатна система, използвана само в равнинно двуизмерно пространство, е полярната координатна система.^[6] Редица криви могат да се опишат много по-лесно чрез полярни, отколкото чрез декартови координати.

Полярната координатна система включва точка в равнината (наричана начало или полюс на координатната система) и лъч (наричан полярна ос). В полярна координатна система с полюс O и полярна ос ${\displaystyle {\vec {o}}}$ на всяка точка M в равнината се съпоставят взаимно еднозначно полярните координати (r, Θ) по следния начин:

• полярната координата r на M е равна на разстоянието между точките M и О
• полярната координата Θ на M е ъгълът, между полярната ос ${\displaystyle {\vec {o}}}$ и лъча ${\displaystyle {\vec {OM}}}$

Ъгловата координата Θ обикновено се измерва в радиани, а по традиция посоката на въртене от полярната ос към точката M, съответстваща на положителни стойности на ъгъла, е обратната на часовниковата стрелка. Полюсът на координатната система O има координати (0, Θ) за произволна стойност на Θ. За да се постигне взаимна еднозначност между точката и нейните координати, ъгълът се ограничава между определени стойности, най-често в интервала [-π, π).

В конкретни задачи полярните координати са използвани в неявен вид от Албрехт Дюрер (1525), Исак Нютон и Якоб Бернули (1691). Първи Леонард Ойлер през 1748 година стига до идеята, че положението на точка в равнината може да се определи само чрез ъгъл и разстояние. Във втората част на неговия труд „Analysis infinitorum“ се появяват формулите за преобразуване на полярни в декартови координати. Самите термини „полюс“ и „полярни координати“ навлизат едва през XIX век с работите на Гаспар Монж и школата му. Полярният ъгъл Θ така и не получава устойчиво название: наричан е „аномалия“, „амплитуда“, „азимут“ и дори „аргумент“.

Цилиндричната координатна система е разширение на концепцията на полярните координати за случая на тримерно пространство. Към двете координати на полярната система, тя добавя трета, равна на разстоянието между точката и равнината, в която се измерват полярните координати.

Цилиндричната координатна система се дефинира от точка О (полюс), нулев лъч ${\displaystyle {\vec {o}}}$ и перпендикулярен втори лъч през точка O – ${\displaystyle {\vec {\nu }}}$. В тази система произволна точка М в тримерното пространство има цилиндрични координати (${\displaystyle r,\theta ,h}$), дефинирани по следния начин:

• цилиндричната координата r (радиус на цилиндъра) на M е равна на разстоянието от точка О до ортогоналната проекция на точка M в равнина, преминаваща през O и перпендикулярна на ${\displaystyle {\vec {\nu }}}$
• цилиндричната координата Θ на M е ъгълът, образуван от лъча ${\displaystyle {\vec {o}}}$ и радиус-вектора на ортогоналната проекция на M в равнина, преминаваща през O и перпендикулярна на ${\displaystyle {\vec {\nu }}}$
• цилиндричната координата h на M е равна на разстоянието между точко M и равнината, преминаваща през O и перпендикулярна на ${\displaystyle {\vec {\nu }}}$

Този вид координати са наречени цилиндрични, понеже r играе ролята на радиус на цилиндър, а h – на неговата височина.

Сферичната координатна система е друга често използвана тримерна координатна система. За разлика от цилиндричните координати, които се състоят от два скалара и един ъгъл, сферичните са един скалар и два ъгъла.

Подобно на цилиндричната координатна система, и сферичната се дефинира от една точка О (полюс или начало координатната система) и два перпендикулярни лъча ${\displaystyle {\vec {e_{1}}}}$ (задаващ нулева посока) и ${\displaystyle {\vec {e_{2}}}}$ (полярна ос, задаваща северна посока), минаващи през точка О. Равнината, определена от двата лъча, се нарича първична меридианна равнина, а равнината, която минава през лъча e₁^→ и е перпендикулярна на лъча e₂^→, се дефинира като екваториална равнина (понякога наричана хоризонтална равнина).

Координатите на всяка точка M от тримерното пространство, се определят чрез 3 координати:

• r – разстоянието полюса O и точката M
• Θ – ъгъла между вектора ${\displaystyle {\vec {OM*}}}$ и лъча ${\displaystyle {\vec {e_{1}}}}$, където M* е ортогоналната проекция на точка M в хоризонталната равнина; обикновено Θ се ограничава в интервал [-π, π), а за положителна се приема посоката на завъртане срещу часовниковата стрелка, гледано от северната посока
• φ – ъгъла между векторите ${\displaystyle {\vec {OM}}}$ и ${\displaystyle {\vec {OM*}}}$; φ се ограничава в интервал [-π/2, π/2], а обикновено за положителна се приема посоката на завъртане в северна посока

Съответствието между точките в пространството и сферичните им координати е взаимно еднозначно, освен за точките по полярната ос, за които ъгълът Θ е неопределен, и за полюса O, за който и двата ъгъла, Θ и φ, са неопределени.

В практиката сферичните координатни системи намират приложение в различни астрономически координатни системи, които използват различни, избрани за определена цел, екваториални равнини (хоризонта на наблюдателя, небесния екватор, равнината на еклиптиката и други). Сферичните координати се използват и в системите за управление на огъня в артилерията, където линейната координата обикновено се нарича разстояние, ъгълът, мерен по равнината – азимут, а този спрямо на нея – ъгъл на възвишение.

Като първо приближение ъгловите сферични координати могат да се ползват и като географски координати, но отклонението на формата на Земята от математическата сфера води до значителни неточности, поради което обикновено в географията и геодезията се използват специализирани координатни системи.

Независимо че сферичните координати са се ползвали в астрономията на древността, първите опити да се дефинира крива върху сфера с уравнение между сферичните им координати е от XVIII в. Трансформационните формули, които изразяват декартовите чрез сферичните, са дадени от Лагранж през 1773 г. Обратните трансформационни формули са изведени от Феликс Клайн през 1881 г.

 Основна статия: Географска координатна система

В географията и геодезията най-често се използват специализирани координатни системи, подобни на сферичната координатна система, които подобно на нея използват за координати два ъгъла и едно разстояние:^[7]

• h – надморска височина; за разлика от сферичната координатна система, тук това е разстоянието от точката не до началото на координатната система, а до определена повърхнина, наричана референц-елипсоид, като точките във вътрешността ѝ имат отрицателна надморска височина
• λ – географска дължина – ъгълът между радиус-вектора на проекцията на точката в екваториалната равнина и равнината на зададен начален меридиан; обикновено се измерва в градуси, в интервала между -180° и +180° (положителните стойности се наричат също и ъгли източна дължина, а отрицателните – западна дължина)
• ϕ – географска ширина – може да бъде дефинирана по два начина, като и в двата случая обикновено се измерва в градуси, в интервала между -90° и 90° (положителните стойности се наричат също и ъгли северна ширина, а отрицателните – южна ширина):
  • геодезическата ширина – по-често използвана – е ъгълът между екваториалната равнина, и права, която преминава през точката и е перпендикулярна на референц-елипсоида
  • геоцентричната ширина е ъгълът между екваториалната равнина, и права, която преминава през точката и през полюса на координатната система (както при сферичните координати)

За полюс на географските координатни системи обикновено се приема предполагаем център на масите на планетата Земя. Те използват различни референц-елипсоиди, които представляват приближения на геоид – сложна повърхнина, дефинирана като перпендикулярна във всяка своя точка на земното гравитационно поле. Най-широко използваната географска координатна системи от тази група е Световната геодезическа система (WGS), която служи за основа и на Глобалната система за позициониране (GPS).

Други координатни системи, използвани за локализиране на точки от земната повърхност, са двуизмерни декартови координатни системи, дефинирани върху определена картографска проекция. Широко използвани системи от този тип са универсалната напречна цилиндрична проекция на Меркатор (UTM) и универсалната полярна стереографска координатна система (UPS).

За нуждите на геодезията се използват и триизмерни декартови координатни системи, дефинирани по различни начини, според целта, за която трябва да послужат. Геоцентричната координатна система е с равнина Oxy в екваториалната равнина, ос z, преминаваща през Северния и Южния полюс и ос x през началния меридиан.Тангенциалната координатна система е с произволно избрано начало O, ос z по посока, обратна на гравитационната сила в точка O, и ос y, насочена към северната посока на правата, преминаваща през двата полюса.

Други координатни системи, които имат специфично приложение, са:

• Криволинейна координатна система – обобщение на координатните системи, в които всички координати са разстояния, тя използва координатни линии, които са произволни криви
  • Ортогонална координатна система – с координатни повърхнини, пресичащи се под прави ъгъли
• Логаритмично-полярна координатна система – подобна на полярната, но използваща логаритъм на разстоянието на точките до полюса
• Хомогенна координатна система – често използвана в проективната геометрия, описваща всички точки в пространството с крайни координати
• Плюкерови координати – използвани за представяне на прави в триизмерното евклидово пространство чрез шесторки от числа, които са хомогенни координати
• Обобщени координати – използвани в механиката на Лагранж
• Канонични координати – използвани в механиката на Хамилтон
• Барицентрична координатна система – използвана в анализа на триъгълници
• Трилинейна координатна система – използвана в контекста на триъгълниците

 Основна статия: Преобразуване на координати

Геометричните обекти могат да бъдат описвани в множество различни координатни системи, като вече известните координати на даден обект в определена координатна система могат да бъдат преобразувани в координати в друга координатна система, обикновено чрез система от формули, задаващи връзката между двете системи. Например, ако в равнината има зададени декартова и полярна координатна система с общо начало и абсциса, съвпадаща с полярната ос, декартовите координати (x, y) могат да се получат от полярните координати (r, θ) чрез зависимостите x = r cosθ и y = r sinθ.

От полярни координати

• ${\displaystyle x=r.cos\theta }$
• ${\displaystyle y=r.sin\theta }$

Тези формули са валидни, когато началото на декартовата координатна система в равнината съвпадне с полюса O и когато положителната посока на оста x^→ съвпадне с положителната посока на лъча o^→.

От цилиндрични координати

• ${\displaystyle x=r.cos\theta }$
• ${\displaystyle y=r.sin\theta }$
• ${\displaystyle z=h}$

Те са в сила, когато за начало на декартовата координатна система е избран полюсът O на цилиндричната, а лъчите ${\displaystyle {\vec {x}}}$ и ${\displaystyle {\vec {z}}}$ от декартовата съвпадат съответно с ${\displaystyle {\vec {o}}}$ и ${\displaystyle {\vec {\nu }}}$ от цилиндричната.

От сферични координати

• ${\displaystyle x=r.cos\varphi .cos\theta }$
• ${\displaystyle y=r.cos\varphi .sin\theta }$
• ${\displaystyle z=r.sin\varphi }$

Тези формули са валидни, когато началото на двете координатни системи съвпада и когато положителните посоки на осите ${\displaystyle {\vec {x}}}$ и ${\displaystyle {\vec {z}}}$ съвпадат съответно с посоките на лъчите ${\displaystyle {\vec {e_{1}}}}$ и ${\displaystyle {\vec {e_{2}}}}$.

От декартови координати

• ${\displaystyle r={\sqrt {x^{2}+y^{2}}}}$
• ${\displaystyle tg\theta ={\frac {y}{x}}}$ (придружено от информация за квадранта, в който се намира точката).

Тези формули са валидни, когато началото на декартовата координатна система в равнината съвпадне с полюса O и когато положителната посока на оста x^→ съвпадне с положителната посока на лъча o^→.

От декартови координати

• ${\displaystyle r={\sqrt {x^{2}+y^{2}}}}$
• ${\displaystyle tg\theta ={\frac {y}{x}}}$ (придружено от информация за квадранта, в който се намира точката)
• ${\displaystyle h=z}$

Те са в сила, когато за начало на декартовата координатна система е избран полюсът O на цилиндричната, а лъчите ${\displaystyle {\vec {x}}}$ и ${\displaystyle {\vec {z}}}$ от декартовата съвпадат съответно с ${\displaystyle {\vec {o}}}$ и ${\displaystyle {\vec {\nu }}}$ от цилиндричната.

• ${\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}$
• ${\displaystyle tg\theta ={\frac {y}{x}}}$(придружено от информация за квадранта, в който се намира точката)
• ${\displaystyle tg\varphi ={\frac {z}{\sqrt {x^{2}+y^{2}}}}}$

Тези формули са валидни, когато началото на двете координатни системи съвпада и когато положителните посоки на осите ${\displaystyle {\vec {x}}}$ и ${\displaystyle {\vec {z}}}$ съвпадат съответно с посоките на лъчите ${\displaystyle {\vec {e_{1}}}}$ и ${\displaystyle {\vec {e_{2}}}}$.

Преобразуването на координати в дадена декартова координатна система в координати в друга декартова система става чрез извършването върху тях на две операции – транслация и ротация.

Когато съответните оси на двете координатни системи са успоредни, транслационната операция е достатъчна и преобразуването на координатите става по следния начин:

${\displaystyle r_{2}=r_{1}-O_{2,1},}$

където ${\displaystyle r_{1}}$ и ${\displaystyle r_{2}}$ са радиус-векторите на точката в първата и втората координатна система, а ${\displaystyle O_{2,1}}$ е радиус-векторът на началото на втората координатна система.

Когато двете координатни системи имат общо начало, преобразуването на координатите става само чрез ротация:

${\displaystyle r_{2}=Rr_{1},}$

където ${\displaystyle r_{1}}$ и ${\displaystyle r_{2}}$ са радиус-векторите на точката в първата и втората координатна система, а ${\displaystyle R}$ е матрица на ротация, която зависи от ъглите между осите на двете координатни системи. При триизмерно пространство матрицата на ротация има вида:^[8]

${\displaystyle R={\begin{bmatrix}\cos \alpha \cos \beta &\cos \alpha \sin \beta \sin \gamma -\sin \alpha \cos \gamma &\cos \alpha \sin \beta \cos \gamma +\sin \alpha \sin \gamma \\\sin \alpha \cos \beta &\sin \alpha \sin \beta \sin \gamma +\cos \alpha \cos \gamma &\sin \alpha \sin \beta \cos \gamma -\cos \alpha \sin \gamma \\-\sin \beta &\cos \beta \sin \gamma &\cos \beta \cos \gamma \\\end{bmatrix}},}$

където ${\displaystyle \alpha }$, ${\displaystyle \beta }$ и ${\displaystyle \gamma }$ са ъглите на Ойлер, описващи взаимното положение на двете координатни системи.

При произволно положение на двете координатни системи транслацията и ротацията се извършват последователно:

${\displaystyle r_{2}=R(r_{1}-O_{2,1})}$

Потребността от използване на координати се появява под различни форми в географията, астрономията и математиката още във Вавилония и Древна Гърция. Познатите ни днес термини за координатните оси обаче започват да се използват със съвременното си значение едва през XVII в.

През XIV в. френският математик Никола Орем е строил графики, използвайки равнинни координати, които наричал „дължина“ и „широчина“ в смисъла на абсциса и ордината.

Терминът абсциса (abscissa) се употребявал широко в латинските преводи от гръцки на математически трудове. Смисълът, който обаче е бил влаган в термина, било „отсечка“. Тази практика се запазва за последно в трудовете на Бонавентура Кавалиери от 1635 г. През 1675 г. Готфрид Лайбниц налага новия прочит на термина абсциса като първа ос на координатната система.

Аполоний (ок. 260 – 170 г. пр.н.е.) нарича успоредните хорди в окръжността „линии прекарани поред“, като превежда словосъчетанието от гръцки на латински като „ordinatum applicata“. Оттук произхождат термините ордината и апликата, като впоследствие изразът се разпада и двете понятия започват да се употребяват самостоятелно в контекста на сечения на кръга.

Думата ордината в съвременния ѝ смисъл като втора координата на точка е използвана за първи път от Лайбниц (1694 г.). Приблизително по това време той въвежда и самия термин координата, като по този начин подчертава равноправието на абсцисата и ординатата.

Малко популярната дума апликата означава третата координатна ос, когато координатната система е пространствена.

Цитирани източници

• Rotation Matrices // continuummechanics.org. continuummechanics.org, 2020. Посетен на 2020-10-11. (на английски)
• Finney, Ross et al. Calculus: Graphical, Numerical, Algebraic. Single Variable Version. Addison-Wesley Publishing Co., June 1994. ISBN 0-201-55478-X. (на английски)
• Moon, P et al. Rectangular Coordinates (x, y, z) // Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions. corrected 2nd, 3rd print. New York, Springer-Verlag, 1988. ISBN 978-0-387-18430-2. (на английски)
• A guide to coordinate systems in Great Britain // Ordnance Survey, Mar 2015. Архивиран от оригинала на 2015-09-24. Посетен на 2015-06-22. (на английски)
• Stewart, James B. et al. College Algebra. 5th. Brooks Cole, 2008. ISBN 0-495-56521-0. (на английски)
• Weisstein, Eric W. Coordinate System // MathWorld. Wolfram Research, 2020a. Посетен на 2020-09-19. (на английски)
• Weisstein, Eric W. Coordinates // MathWorld. Wolfram Research, 2020b. Посетен на 2020-09-19. (на английски)
• Woods, Frederick S. Higher Geometry. Ginn and Co., 1922. (на английски)

• Декартова координатна система
• Полярна координатна система

Нормативен контрол BNF GND NLI J9U LCCN LNB