Фрактал – Уикипедия

Фракталът е структура, за която се установява нетривиално самоподобие със собствените ѝ части. В много отношения това контрастира с обичайните „гладки“ обекти в традиционната математика и геометрия. Фракталът се представя като геометричен обект, който е радикално „начупен“. Терминът фрактал (от латинското fractus, счупен) е въведен през 1975 от Беноа Манделброт, за да привлече вниманието към тези обекти^[1]. Като математически куриози те са известни още от 19 в.

Строго погледнато, фракталите са начупени в произволно малки мащаби, така че реално могат да бъдат изобразявани само техни крайни апроксимации. Най-често фракталът се генерира (например на монитор) от повтаряща се схема, обикновено рекурсивен или итерационен процес. Това позволява представяне на неговите характерни особености – самоподобността и възпроизвеждането на цялостната структура независимо от увеличението.

Често привеждани примери за фрактали са множеството на Манделброт, канторовото множество, триъгълникът и килимът на Сиерпински, кривата на Пеано и снежинката на Кох. Срещани често в природата обекти като облаци, планини, водосборни басейни или кръвоносни системи, са примери за приблизителни фрактали, тъй като имат горна и долна граница на увеличението. Типичен природен фрактал е формата на римското зеле.

Различни видове фрактали са изучавани първоначално като математически обекти и терминът „фрактал“ е получил различни определения. „Фракталната геометрия“ е неформална област от математиката, в която са събрани разнородни елементи свързвани с изучаване на фракталите и особеното им поведение^[2]. Тя намира приложение в науката, техниката и компютърното изкуство.

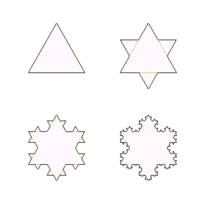
Обекти, които днес се наричат фрактали, са открити и изследвани дълго преди появата на самата дума. През 1872 Карл Вайерщрас открива пример за функция с неинтуитивното свойство да е непрекъсната навсякъде без да е диференцируема никъде (Функция на Вайерщрас). Графиката на тази функция в наши дни би била наречена фрактал. През 1904 Хелге фон Кох, недоволен от твърде абстрактната и аналитична дефиниция на Вайерщрас, дава по-геометрично определение на подобна функция, която днес се нарича снежинка на Кох. Идеята за самоподобни криви е доразвита от Пол Пиер Леви. През 1938 той публикува Равнинни или пространствени криви и повърхнини, състоящи се от части, подобни на цялото, където описва две фрактални криви – C-крива на Леви и драконова крива на Леви.

Георг Кантор дава примери за подмножества на реалната права с необичайни свойства. Тези канторови множества (Прах на Кантор) също днес се определят като фрактали. Опитвайки се да разберат обекти, подобни на канторовите множества, математици като Константин Каратеодори и Феликс Хаусдорф обобщават интутивната идея за размерност като включват и не цели стойности (фрактална размерност). Итеративни функции в комплексната равнина са изследвани в края на 19 и началото на 20 век от Анри Поанкаре, Феликс Клайн, Пиер Фату и Гастон Жулиа. Без помощта на съвременната компютърна графика, обаче, те не са имали възможността да визулизират откритите от тях обекти.

През 1960-те Беноа Манделброт започва да изследва самоподобността и публикува своята статия озаглавена Колко дълго е крайбрежието на Великобритания? Статистическа самоподобност и дробна размерност^[3]. Осланяйки се на визуални аналогии, Манделброт упява да установи връзка между елементи на математиката, несвързвани дотогава. Научно-популярната книга, ^[4] в която излага своите идеи и търсения, добива световна известност. След нейното излизане, през 1975, той започва да употребява съществителното фрактал.

Прилагането на компютърна визуализация към фракталната геометрия дава силен визуален аргумент за връзките на фракталната геометрия с далеч по-широки области на математиката и науката, отколкото се е смятало преди това, особено в областта на нелинейната динамика, теорията на хаоса и комплексните системи. Пример за това е нютоновият фрактал – изобразяване на характеристики на решението по метода на Нютон като фрактал, което показва как границите между различните решения са фрактали, а самите решения са странни атрактори. Фракталната геометрия се използва и при компресиране на данни и моделиране на сложни органични и геоложки системи, например растежа на дърветата или развитието на речните басейни.

Люис Фрай Ричардсън е пацифист и математик, изучавал причините за войната между две страни. Той решава да потърси зависимостта между размера на общата им граница и вероятността две страни да влязат във война. Като част от своята работа, той изследва как се изменя получената дължина на границата при промяна на единицата за измерване. Той публикува емпирична статистика, цитирана по-късно от Манделброт в неговата работа Колко дълго е крайбрежието на Великобритания? Статистическа самоподобност и дробна размерност^[3].

Да предположим, че крайбрежието на остров Великобритания се измерва с единица мярка 200-километрова отсечка, като двата края на отсечката едновременно опират в брега (можем да си представим, че измерваме с пергел с такъв разтвор). След това отсечката се намалява наполовина и процесът на измерване се повтаря, а след това се намалява на една четвърт от първоначалната и т.н.

Забелязва се, че колкото по-малка е отсечката, толкова по-голям е крайният резултат. Може да се предположи, че тези стойности ще клонят към някакво крайно число, което ще е „реалната“ дължина на крайбрежието, но Ричардсън доказва, че всъщност измерванията на дължината на бреговата линия клонят към безкрайност.

Тези изследвания на Ричардсън са игнорирани от научната общност до публикацията на Манделброт през 1967. Днес те се считат за част от началото на съвременните изследвания на фракталите.

350-кратното увеличение на множеството на Манделброт разкрива подробност, наподобяваща пълното множество.

Фракталите могат да се групират в три общи категории, според начина на дефиниране и генериране:

• Системите от итеративни функции имат фиксирано правило за геометрично отместване (канторово множество, килим на Сиерпински, въже на Сиерпински, крива на Пеано, снежинка на Кох, драконова крива на Леви).
• Фрактали, определени от рекурсивна зависимост във всяка точка от дадено пространство (например комплексната равнина). Примери за този вид са множеството на Манделброт и фракталът на Ляпунов. Понякога тези фрактали се наричат фрактали с време на излизане.
• Случайните фрактали са генерирани от стохастичен, а не от детерминистичен процес, например фракталните пейзажи и полетите на Леви.

Фракталите могат да се класифицират и според самоподобността. Наблюдават се три вида самоподобност:

• Точна самоподобност – най-силната самоподобност. Фракталът е идентичен в различни мащаби. Фракталите, дефинирани от итеративни функции, често притежават това свойство.
• Квазисамоподобност – по-слаба форма на самоподобност, при която фракталът изглежда приблизително, но не напълно, идентичен в различни мащаби. Квазисамоподобните фрактали съдържат малки копия на целия фрактал в деформирани и изродени форми. Фракталите, дефинирани от рекурсивни функции обикновено са квазисамоподобни, но не точно самоподобни.
• Статистическа самоподобност – най-слабата форма на себеподобност. Фракталът има числени или статистически характеристики, които се запазват в различни мащаби. Най-убедителната дефиниция на „фрактал“ предполага някаква форма на самоподобност. Самата фрактална размерност е числена характеристика, която се запазва в различните мащаби. Случайните фрактали са пример за статистическа самоподобност.

Трябва да се отбележи, че не всички самоподобни обекти са фрактали. Например реалната права е точно самоподобна, но идеята, че евклидовите обекти са фрактали, се споделя от малцина. Според Манделброт дефиницията на „фрактал“ трябва да включва не само „истинските“ фрактали, но и традиционните евклидови обекти, тъй като ирационалните числа на числовата права имат сложни непериодични свойства.

Тъй като фракталите имат безкрайно фина структура, никой естествен обект не може да бъде фрактал. Въпреки това, някои естествени обекти проявяват свойства, сходни на тези на фракталите, но в ограничен обхват на мащаба.

Специфичните характеристики на фракталите, макар и интуитивно разбираеми, са извънредно трудни за прецизно математическо дефиниране. Проблемите с дефинирането на фракталите включват:

• няма точно значение на „прекалено неравномерен“
• няма единствено определение на „размерност“
• има много начини, по които един обект може да бъде самоподобен
• не всеки фрактал е дефиниран рекурсивно

Следните дефиниции на фрактал са предлагани, но всяка от тях си има недостатъци:

• Обект, който е самоподобен в някакъв смисъл (включително нелинейната самоподобност и статистическата самоподобност) – това е проста интуитивна дефиниция, но е много трудно да се прецизира математически. Тя също включва и обектите на традиционната евклидова геометрия, които по принцип не се считат за фрактали.

• Обект с не-цяла хаусдорфова размерност – но това изключва някои обекти, които по принцип се считат за фрактали, като кривата на Пеано и границата на множеството на Манделброт.

• Множество с хаусдорфова размерност, която строго надхвърля неговата топологична размерност – това е най-широко възприетата математическа дефиниция, но изисква известна математическа подготовка, за да бъде разбрана.

Дърветата и папратите са естествени фрактали и могат да бъдат компютърно моделирани с рекурсивни алгоритми. Рекурсивната им природа проличава от следния пример – ако се вземе отделен клон от дърво или лист от папрат, може да се види, че то е миниатюрно копие на цялото, не идентично, но подобно по същество.

Сравнително проста група примери са канторовите множества, при които все по-малки отворени интервали са изваждани от единичния интервал [0, 1], оставяйки множество, което може да бъде (или да не бъде) самоподобно при увеличение и може да има (или да няма) размерност d, за което 0 < d < 1. Просто правило, като изключването на цифрата 7 от десетичните дроби, генерира множество, което е самоподобно при 10-кратно увеличение и има размерност log 9/log 10 (стойността се запазва, независимо от основата на логаритъма), и така демонстрира връзката между двете концепции.

Фракталите по принцип са с неравномерна (не гладка) форма и, следователно, не са обекти, дефинируеми от традиционната геометрия. Това означава, че те имат значителна подробност, забележима при произволен мащаб. Самоподобността се явява, защото приближението просто разкрива сходна картина. Такива множества обикновено се дефинират чрез рекурсия.

Например една обичайна евклидова фигура като окръжността изглежда все по-плоска при увеличение. При безкрайно увеличение, би било невъзможно окръжността да се отличи от правата. Фракталите са различни. Обичайната концепция за кривина, представляваща реципрочната стойност на радиуса на апроксимирана окръжност, е неприложима. При фракталите увеличението разкрива подробности, незабележими преди това.

Някои обичайни примери за фрактали са множеството на Манделброт, фракталът на Ляпунов, канторовото множество, килимът и триъгълникът на Сиерпински, кривата на Пеано и снежинката на Кох.

Приблизителни фрактали се срещат често в природата. Тези обекти имат сложна структура в широк, но ограничен, обхват на мащаба. Тези естествено срещащи се фрактали, като облаци, планини, водосборни басейни и кръвоносни системи, имат горна и долна граница на увеличението.

• Фрактално изкуство
• Фрактален пейзаж
• Графтал
• Алгоритъм диамант-квадрат
• Хаусдорфова размерност
• Гастон Жулиа
• Беноа Манделброт
• Нелинейна динамика
• Турбулентност
• Теория на хаоса

на български език

• Фракталите. За математиката на природата.
• Еволюцията и хаосът. За произхода на живота Архив на оригинала от 2012-04-10 в Wayback Machine..
• Някои идеи за практическо приложение на фракталните изображения
• Фрактална анимация. Множество на Манделброт.
• Фрактална анимация. Метод на Нютон
• Фрактална анимация и електронна музика
• Маргарита Серафимова, Съдържанието на формите: изкуство и фракталност

на английски език

• Фрактали, фрактална размерност, хаос, криви, запълващи равнината
• Свойства на фракталите Архив на оригинала от 2006-09-01 в Wayback Machine.
• Информация за фракталите от FAQS.org
• Примери на фрактали Архив на оригинала от 2005-08-31 в Wayback Machine.
• Фрактално изкуство Архив на оригинала от 2005-12-12 в Wayback Machine.
• Фрактални пейзажи Архив на оригинала от 2015-08-01 в Wayback Machine.
• Фрактална размерност
• Фрактален анализ Архив на оригинала от 2012-04-20 в Wayback Machine.
• Гравитационно множество на Мичъл-Грийн Архив на оригинала от 2005-09-01 в Wayback Machine.
• Начало на фрактална индустрия