Rayleigh-Bénard-Konvektion – Wikipedia

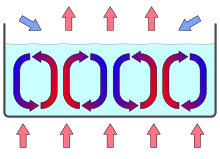
Die Rayleigh-Bénard-Konvektion ist eine natürliche Konvektion in flachen Flüssigkeiten mit einem speziellen Zellenmuster. In den Bénard-Zellen steigt die Flüssigkeit im Zentrum auf, kühlt sich an der Oberfläche durch Verdunstung ab und sinkt mit erhöhter Dichte am Zellenrand wieder zum Boden.

Der französische Physiker Henri Bénard beschrieb dies 1900 in seiner Dissertation^[1][2][3] und der englische Physiker John William Strutt, 3. Baron von Rayleigh formulierte 1916 den Vorgang mathematisch.^[4]

Die Rayleigh-Bénard-Konvektion ist ein Beispiel für selbstorganisierende Strukturen und die Chaostheorie. Sie ist nicht mit dem Marangoni-Effekt zu verwechseln, der auf der Oberflächenspannung basiert.

Ist die Temperaturdifferenz ${\displaystyle \Delta T}$ zwischen Boden und Oberfläche gering, so überwiegen zunächst noch die Kräfte infolge der Viskosität und die Wärme wird ohne gleichzeitigen Stofftransport nur durch Wärmeleitung von unten nach oben befördert.

Oberhalb eines kritischen Temperaturunterschiedes ${\displaystyle \Delta T_{{\text{krit}},1}}$ wird dieser Zustand jedoch instabil, der Wärmetransport findet dann durch Wärmekonvektion statt. Die Flüssigkeit kommt aufgrund der Dichteunterschiede zwischen Ober- und Unterseite in Bewegung: an der warmen Unterseite dehnt sie sich aus und steigt aufgrund der geringeren Dichte nach oben, während die kältere, dichtere Flüssigkeit im oberen Bereich absinkt. Die Viskosität begrenzt die Geschwindigkeit dieser Bewegungen. Die Konvektions- oder Bénard-Zellen sind von oben gesehen meist polygonal und bilden seitlich Rollenmuster.

Der Zustand, an dem das Fluid instabil wird, kann auch über die Rayleigh-Zahl ${\displaystyle Ra}$ bestimmt werden. Oberhalb der kritischen Rayleigh-Zahl ${\displaystyle Ra_{c}}$ beginnt die Konvektion.

Wenn oberhalb der Flüssigkeit eine Grenzfläche zu einem gasförmigen Medium existiert, wird der konvektive Wärmetransport durch mögliche Unterschiede in der Oberflächenspannung an der Grenzfläche verstärkt. Da die Spannung in der Regel mit der Temperatur abnimmt, besitzen Stellen, die sich näher an einer heißen Gefäßwand befinden, eine kleinere Oberflächenspannung als die weiter von der Wand entfernten. Es entsteht eine zusätzliche Treibkraft, die eine Strömung in Richtung kälterer Bereiche induziert (Marangoni-Konvektion).

Steigt die Temperaturdifferenz zwischen Ober- und Unterseite der Flüssigkeit weiter an, so setzen ab einem zweiten kritischen Wert ${\displaystyle \Delta T_{{\text{krit}},2}}$ Periodenverdopplungen ein. Das dynamische System gelangt auf der Feigenbaum-Route ins Chaos, es entwickelt sich Turbulenz, wie zuerst Albert J. Libchaber Ende der 1970er Jahre zeigte.

Zur Durchführung des Experiments eignen sich besonders Flüssigkeiten mit einer geringen relevanten Viskosität, dünnes Öl oder Gel. Es wurde schon mit flüssigem, tiefgekühltem Helium durchgeführt. Der Wärmeausdehnungskoeffizient der Flüssigkeit muss positiv sein. Das Temperatur- und Strömungsgeschwindigkeits-Feld dieses Experiments muss der Navier-Stokes-Gleichung, der Wärmeleitungsgleichung und der Kontinuitätsgleichung (Erhaltungssatz der Masse) genügen.

Die weltweit größte Simulationsanlage für das Experiment ist das Ilmenauer Fass, eine Einrichtung der Technischen Universität Ilmenau.^[5]

Das Bénard-Experiment ist ein Standardbeispiel für die Ausbildung dissipativer Strukturen in konvektiven, offenen Systemen fern vom thermodynamischen Gleichgewicht. Ähnliches Verhalten kann im Prinzip in allen viskosen Medien auftreten. Neben Modellexperimenten mit dünnen Ölschichten kann man ähnliches Verhalten im Ozean, im Erdmantel als Mantelkonvektion, oder in der Atmosphäre in Form von sechseckigen oder rollenförmigen Wolkenstrukturen entdecken. Die Granulation auf der Sonnenoberfläche oder die Entmischung von Pigmenten mit unterschiedlichen Dichten in bestimmten Lacken während der Trocknung beruhen ebenfalls auf diesem Effekt.

Die Untersuchung der atmosphärischen Konvektion war der Ausgangspunkt, der Anfang der 1960er Jahre zur Entdeckung des deterministischen Chaos durch den Meteorologen Edward Lorenz führte. Er untersuchte den Übergang der Wärmekonvektion in einen turbulenten Zustand innerhalb eines Mediums. Das von ihm zu diesem Zweck aufgestellte System aus drei autonomen Differentialgleichungen (Lorenz-Attraktor) zeigte erstmals am Computer nachvollziehbar chaotische Schwingungen innerhalb eines deterministischen Systems.

• Edward Lorenz: Deterministic nonperiodic flow. In: Journal of the Atmospheric Sciences. 20/1963, S. 130–141.
• Gottfried Jetschke: Mathematik der Selbstorganisation. Verlag Harri Deutsch, Frankfurt a. M. 1989, ISBN 3-8171-1282-3.

• Turbulente rotierende Konvektion (Technische Universität Eindhoven, Niederlande; englisch) mit Darstellung einer präzisierten Rayleigh-Bénard-Zelle nach L. Kadanoff
• Wärmebild (Youtube, Video; deutsch) Wärmebildvideo des Bénard-Effekts in warmen Wasser und kaltem Öl
• A. Getling, O. Brausch: Cellular flow patterns and their evolutionary scenarios in three-dimensional Rayleigh-Bénard convection. In: Phys. Rev. E. Band 67, 2003, S. 046313, doi:10.1103/PhysRevE.67.046313 (englisch, magnetosphere.ru [PDF; 341 kB]). 
• Video: Experiment der Woche: Was haben Benard-Zellen mit Kochen zu tun?. Leibniz Universität Hannover 2011, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/391.

1. ↑ Henri Bénard: Les tourbillons cellulaires dans une nappe liquide. Revue Générale des Sciences 11 (1900), 1261–1271, 1309–1328.
2. ↑ Henri Bénard: Les tourbillons cellulaires dans une nappe liquide transportent de la chaleur par convection en régime permanent. Annales de Chimie Physique 7(23)(1900), 62.
3. ↑ Henri Bénard: Les tourbillons cellulaires dans une nappe liquide: Méthodes optiques d'observation et d'enregistrement. Journal de Physique Théorique et Appliquée 10(1)(1901), 254.
4. ↑ Lord Rayleigh O.M. F.R.S. (1916): LIX. On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Philosophical Magazine Series 6, 32:192, 529–546.
5. ↑ TU Ilmenau, Fakultät für Maschinenbau: Ilmenauer Fass.