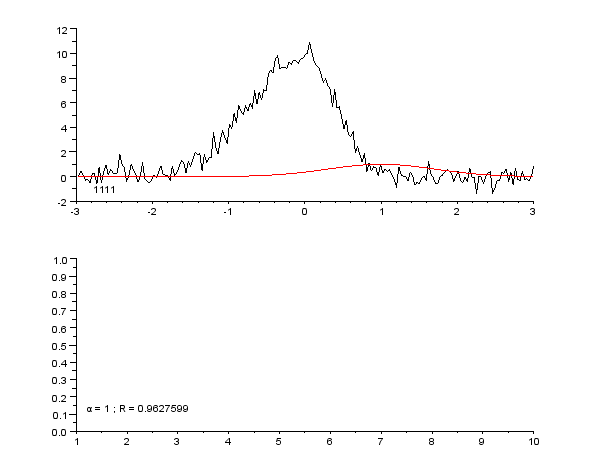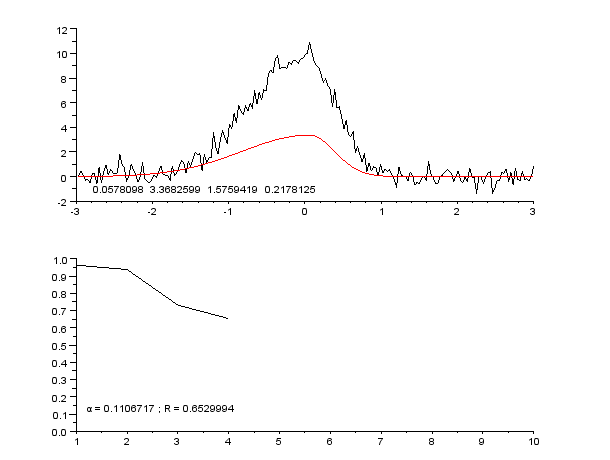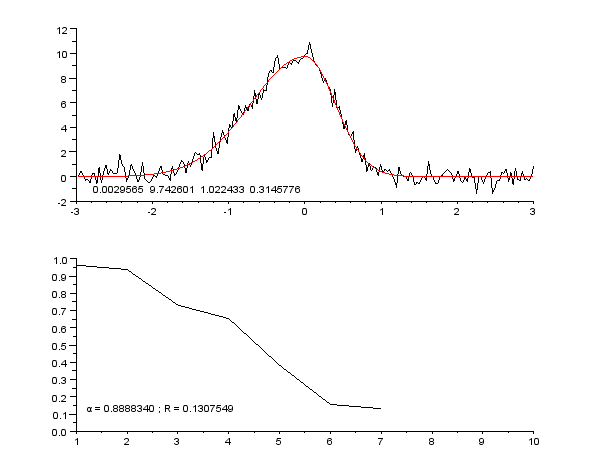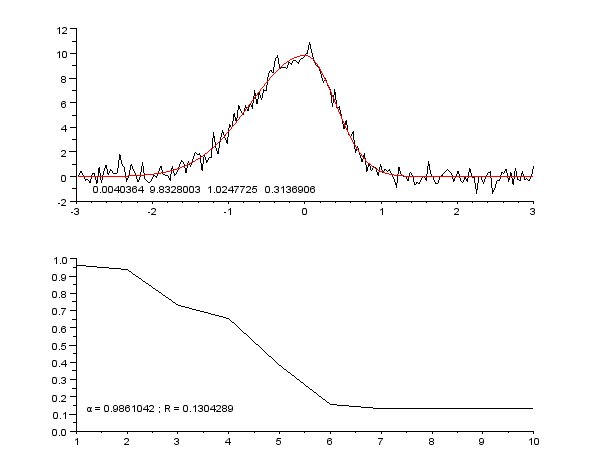
// ********** // Constantes et initialisation // ********** clear; clf; chdir('monchemin/') // Paramètres de Newton-Raphson precision = 1e-7; // condition d'arrêt itermax = 60; // idem // Précision de la linéarisation approchée epsilon = 1e-6; // ********** // Fonctions // ********** exec('fonctions_communes.sce', -1) function [e] = res(Yexp, Ycal) e = sqrt(sum((Yexp-Ycal).^2)); endfunction function [A, R] = gaussnewton(f, X, Yexp, A0, imax, epsilon) // A : jeu de paramètres optimisé par régression (vecteur) // R : liste des facteurs de qualité de la régression // pour chaque étape (vecteur) // X : variable explicative (vecteur) // Yexp : variable expliquée, valeurs mesurées (vecteur) // A0 : paramètres d'initialisation du modèle (vecteur) // epsilon : valeur d'arrêt (scalaire) k = 1; // facteur d'amortissement initial, <=1, // évite la divergence n = size(X,'*'); e0 = sqrt(sum(Yexp.^2)); // normalisation du facteur de qualité Ycal = f(A0, X); // modèle initial R(1) = res(Yexp, Ycal)/e0; // facteur de qualité initial disp('i = 1 ; k = 1 ; R = '+string(R(1))) // affichage param initiaux i = 1; B = A0; subplot(2,1,1) plot2d(X, Yexp, rect=[-3, -2, 3, 12]) plot(X, Ycal, "-r") xstring(-2.8, -1.5, string(B)) subplot(2,1,2) plot2d(R, rect=[1, 0, 10, 1]) xstring(1.2, 0.1, 'α = '+string(k)+' ; R = '+string(R(i))) nom = 'picassym'+string(i)+'.gif'; xs2gif(0,nom) drapeau = %t; while (i < imax) & drapeau // teste la convergence globale i = i+1; deltay = Yexp - Ycal; J = linearisation_approchee(f, B, X, epsilon); // matrice jacobienne tJ = J'; // transposée deltap0 = inv((tJ*J))*tJ*deltay; drapeau2 = %t // pour une 1re exécution while drapeau2 & (k>0.1) // teste la divergence sur 1 étape deltap = k*deltap0; Bnouveau = B + deltap'; Ycal = f(Bnouveau, X); R(i) = res(Yexp, Ycal)/e0; drapeau2 = (R(i) >= R(i-1)) // vrai si diverge if drapeau2 then k = k*0.75; // atténue si diverge else k0 = k; // pour affichage de la valeur k = (1 + k)/2; // réduit l'atténuation si converge end end B = Bnouveau; drapeau = abs(R(i-1) - R(i)) > epsilon clf; subplot(2,1,1) plot2d(X, Yexp, rect=[-3, -2, 3, 12]) plot(X, Ycal, "-r") xstring(-2.8, -1.5, string(B)) subplot(2,1,2) plot2d(R, rect=[1, 0, 10, 1]) xstring(1.2, 0.1, 'α = '+string(k0)+' ; R = '+string(R(i))) nom = 'picassym'+string(i)+'.gif'; xs2gif(0,nom) // disp('i = '+string(i)+' ; k = '+string(k0)+' ; R = '+string(R(i))) end A = B; endfunction // ********** // Programme principal // ********** // lecture des données donnees = read('pic_gauss_dissym_bruite.txt',-1,2); // carcatéristiques des données Xdef = donnees(:,1); Ydef = donnees(:,2); // Ainit = [-0.03, 9.7, 8*((0.84 - 0.03)/2.35)^2, 8*((0.45 + 0.03)/2.35)^2]; Ainit = [1, 1, 1, 1]; // Régression tic(); [Aopt, Rnr] =... gaussnewton(gauss_dissym, Xdef, Ydef,... Ainit, itermax, precision) t = toc(); // Courbe calculée Yopt = gauss_dissym(Aopt, Xdef); // Affichage print(%io(2),Ainit) print(%io(2),Aopt) print(%io(2),t) clf subplot(2,1,1) plot(Xdef, Ydef, "-b") plot(Xdef, Yopt, "-r") subplot(2,1,2) plot(Rnr) 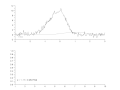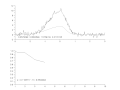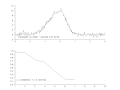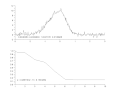



 French
French Deutsch
Deutsch