Dreiecksungleichung – Wikipedia

Die Dreiecksungleichung ist in der Geometrie ein Satz, der besagt, dass eine Dreiecksseite höchstens so lang wie die Summe der beiden anderen Seiten ist. Das „höchstens“ schließt dabei den Sonderfall der Gleichheit ein. Die Dreiecksungleichung spielt auch in anderen Teilgebieten der Mathematik wie der Linearen Algebra oder der Funktionalanalysis eine wichtige Rolle.

Nach der Dreiecksungleichung ist im Dreieck die Summe der Längen zweier Seiten ${\displaystyle a}$ und ${\displaystyle b}$ stets mindestens so groß wie die Länge der dritten Seite ${\displaystyle c}$:

${\displaystyle c\leq a+b}$.

Man kann auch sagen, der Abstand von A nach B ist stets höchstens so groß wie der Abstand von A nach C und von C nach B zusammen, oder um es alltagssprachlich auszudrücken: „Der direkte Weg ist immer der kürzeste.“

Das Gleichheitszeichen gilt dabei nur, wenn ${\displaystyle a}$ und ${\displaystyle b}$ Teilstrecken von ${\displaystyle c}$ sind – man spricht dann auch davon, dass das Dreieck „entartet“ sei.

Da aus Symmetriegründen auch ${\displaystyle a\leq c+b}$ gilt, folgt ${\displaystyle a-b\leq c}$, analog erhält man ${\displaystyle b-a\leq c}$, insgesamt also

${\displaystyle \left|a-b\right|\leq c\leq a+b}$.

Die linke Ungleichung ${\displaystyle \left|a-b\right|\leq c}$ wird gelegentlich auch als umgekehrte Dreiecksungleichung bezeichnet.

Die Dreiecksungleichung charakterisiert Abstands- und Betragsfunktionen. Sie wird daher als ein Axiom für abstrakte Abstandsfunktionen in metrischen Räumen gesetzt.

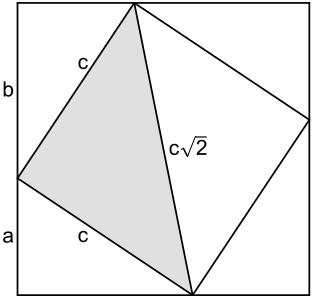
Ist ${\displaystyle c}$ die Hypotenusenlänge und sind ${\displaystyle a}$ und ${\displaystyle b}$ die Kathetenlängen eines rechtwinkligen Dreiecks, so gilt die spezielle Dreiecksungleichung ${\displaystyle a+b\leq c{\sqrt {2}}}$.^[1][2]

• 
  Veranschaulichung für den Fall der Ungleichheit
• 
  Veranschaulichung für den Fall der Gleichheit

Für reelle Zahlen ${\displaystyle a}$ und ${\displaystyle b}$ gilt: ${\displaystyle |a+b|\leq |a|+|b|.}$

Beweis

Seien ${\displaystyle a}$ und ${\displaystyle b}$ reelle Zahlen. Entweder es ist ${\displaystyle a+b\geq 0}$ oder es ist ${\displaystyle a+b<0}$. Für den Fall ${\displaystyle a+b\geq 0}$ gilt ${\displaystyle |a+b|=a+b}$, und die Summe ${\displaystyle a+b}$ lässt sich wegen ${\displaystyle a\leq |a|}$ und ${\displaystyle b\leq |b|}$ nach oben abschätzen durch ${\displaystyle a+b\leq |a|+|b|}$. Insgesamt folgt somit ${\displaystyle |a+b|\leq |a|+|b|}$. Für den Fall ${\displaystyle a+b<0}$ gilt ${\displaystyle |a+b|=-(a+b)=-a-b}$, und ${\displaystyle -a-b}$ lässt sich wegen ${\displaystyle -a\leq |a|}$ und ${\displaystyle -b\leq |b|}$ ebenfalls durch ${\displaystyle |a|+|b|}$ nach oben abschätzen, so dass auch in diesem Fall ${\displaystyle |a+b|\leq |a|+|b|}$.

Wie beim Dreieck lässt sich auch eine umgekehrte Dreiecksungleichung herleiten:

Aufgrund der Dreiecksungleichung gilt ${\displaystyle |a+b|-|b|\leq |a|.}$ Einsetzen von ${\displaystyle a:=x+y,\ b:=-y}$ gibt

${\displaystyle |x|-|y|\leq |x+y|.}$

Setzt man stattdessen ${\displaystyle b:=-x}$ so ergibt sich

${\displaystyle |y|-|x|\leq |x+y|,}$

zusammen also (denn für beliebige reelle Zahlen ${\displaystyle u}$ und ${\displaystyle c}$ mit ${\displaystyle u\leq c}$ und ${\displaystyle -u\leq c}$ gilt auch ${\displaystyle |u|\leq c}$)

${\displaystyle {\Big |}|x|-|y|{\Big |}\leq |x+y|\leq |x|+|y|.}$

Ersetzt man ${\displaystyle y}$ durch ${\displaystyle -y,}$ so erhält man auch

${\displaystyle {\Big |}|x|-|y|{\Big |}\leq |x-y|\leq |x|+|y|.}$

Insgesamt also

${\displaystyle {\Big |}|x|-|y|{\Big |}\leq |x\pm y|\leq |x|+|y|}$ für alle ${\displaystyle x,\,y\in \mathbb {R} .}$

Für komplexe Zahlen gilt:

${\displaystyle |z_{1}{}+z_{2}|\leq |z_{1}|{+}|z_{2}|.}$

Beweis

Da alle Seiten nichtnegativ sind, ist Quadrieren eine Äquivalenzumformung und man erhält

${\displaystyle z_{1}{\overline {z_{1}}}{+}z_{1}{\overline {z_{2}}}{+}{\underbrace {{\overline {z_{1}}}z_{2}} _{={\overline {z_{1}{\overline {z_{2}}}}}}}{+}z_{2}{\overline {z_{2}}}\ \leq \ z_{1}{\overline {z_{1}}}{+}2{\underbrace {|z_{1}z_{2}|} _{=|z_{1}{\overline {z_{2}}}|}}{+}z_{2}{\overline {z_{2}}},}$

wobei der Überstrich komplexe Konjugation bedeutet. Streicht man identische Terme und setzt ${\displaystyle z{\mathrel {:=\,}}z_{1}{\overline {z_{2}}},}$ so bleibt

${\displaystyle z{+}{\bar {z}}\leq 2{|z|}}$

zu zeigen. Mit ${\displaystyle z=u{+}iv}$ erhält man

${\displaystyle (u{+}iv){+}(u{-}iv)=2u\leq 2{\sqrt {u^{2}{+}v^{2}}}}$

bzw.

${\displaystyle |u|\leq {\sqrt {u^{2}{+}v^{2}}},}$

was wegen ${\displaystyle 0\leq v^{2}\ }$ und der Monotonie der (reellen) Wurzelfunktion immer erfüllt ist.

Analog zum reellen Fall folgt aus dieser Ungleichung auch

${\displaystyle {\Big |}|z_{1}|{-}|z_{2}|{\Big |}\leq |z_{1}{\pm }z_{2}|\leq |z_{1}|{+}|z_{2}|}$ für alle ${\displaystyle z_{1},\,z_{2}\in \mathbb {C} .}$

Zusammen mit anderen Forderungen wird eine Betragsfunktion für einen Körper ${\displaystyle K}$ auch durch die

Dreiecksungleichung

${\displaystyle \varphi (x+y)\leq \varphi (x)+\varphi (y)}$

etabliert. Sie hat zu gelten für alle ${\displaystyle x,y\in K.}$ Sind alle Forderungen (s. Artikel Betragsfunktion) erfüllt, dann ist ${\displaystyle \varphi }$ eine Betragsfunktion für den Körper ${\displaystyle K.}$

Ist ${\displaystyle \varphi (n)\leq 1}$ für alle ganzen ${\displaystyle n:=\underbrace {1+\dots +1} _{n{\text{-mal}}}}$, dann nennt man den Betrag nichtarchimedisch, andernfalls archimedisch.

Bei nichtarchimedischen Beträgen gilt die

verschärfte Dreiecksungleichung

${\displaystyle \varphi (x+y)\leq \max(\varphi (x),\varphi (y)).}$

Sie macht den Betrag zu einem ultrametrischen. Umgekehrt ist jeder ultrametrische Betrag nichtarchimedisch.

Mehrmalige Anwendung der Dreiecksungleichung bzw. vollständige Induktion ergibt

${\displaystyle \left|\sum _{i=1}^{n}x_{i}\right|\leq \sum _{i=1}^{n}\left|x_{i}\right|}$

für reelle oder komplexe Zahlen ${\displaystyle x_{i}\;}$. Diese Ungleichung gilt auch, wenn Integrale anstelle von Summen betrachtet werden:

Ist ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ eine Riemann-integrierbare Funktion, dann gilt

${\displaystyle \left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx}$.^[3]

Dies gilt auch für komplexwertige Funktionen ${\displaystyle f\colon [a,b]\to \mathbb {C} }$, vgl.^[4] Dann existiert nämlich eine komplexe Zahl ${\displaystyle \alpha }$, so dass

${\displaystyle \alpha \int _{a}^{b}f(x)\,dx=\left|\int _{a}^{b}f(x)\,dx\right|}$ und ${\displaystyle |\alpha |=1\;}$.

Da

${\displaystyle \left|\int _{a}^{b}f(x)\,dx\right|=\alpha \int _{a}^{b}f(x)\,dx=\int _{a}^{b}\alpha \,f(x)\,dx=\int _{a}^{b}\operatorname {Re} (\alpha f(x))\,dx+i\,\int _{a}^{b}\operatorname {Im} (\alpha f(x))\,dx}$

reell ist, muss ${\displaystyle \int _{a}^{b}\operatorname {Im} (\alpha f(x))\,dx}$ gleich Null sein. Außerdem gilt

${\displaystyle \operatorname {Re} (\alpha f(x))\leq |\alpha f(x)|=|f(x)|}$,

insgesamt also

${\displaystyle \left|\int _{a}^{b}f(x)\,dx\right|=\int _{a}^{b}\operatorname {Re} (\alpha f(x))\,dx\leq \int _{a}^{b}|f(x)|\,dx}$.

Für Vektoren gilt:

${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|\leq \left|{\vec {a}}\right|+\left|{\vec {b}}\right|}$.

Die Gültigkeit dieser Beziehung sieht man durch Quadrieren

${\displaystyle \left|{\vec {a}}+{\vec {b}}\right|^{2}=\left\langle {\vec {a}}+{\vec {b}},{\vec {a}}+{\vec {b}}\right\rangle =\left|{\vec {a}}\right|^{2}+2\left\langle {\vec {a}},{\vec {b}}\right\rangle +\left|{\vec {b}}\right|^{2}\leq \left|{\vec {a}}\right|^{2}+2\left|{\vec {a}}\right|\left|{\vec {b}}\right|+\left|{\vec {b}}\right|^{2}=\left(\left|{\vec {a}}\right|+\left|{\vec {b}}\right|\right)^{2}}$,

unter Anwendung der Cauchy-Schwarzschen Ungleichung:

${\displaystyle \langle {\vec {a}},{\vec {b}}\rangle \leq \left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|}$.

Auch hier folgt wie im reellen Fall

${\displaystyle {\Big |}\left|{\vec {a}}\right|-\left|{\vec {b}}\right|\,\,{\Big |}\leq \left|{\vec {a}}\pm {\vec {b}}\right|\leq \left|{\vec {a}}\right|+\left|{\vec {b}}\right|}$

sowie

${\displaystyle \left|\sum _{i=1}^{n}{\vec {a}}_{i}\right|\leq \sum _{i=1}^{n}\left|{\vec {a}}_{i}\right|.}$

In sphärischen Dreiecken gilt die Dreiecksungleichung im Allgemeinen nicht.

Sie gilt jedoch, wenn man sich auf eulersche Dreiecke beschränkt, also solche, in denen jede Seite kürzer als ein halber Großkreis ist.

In nebenstehender Abbildung gilt zwar

${\displaystyle \left|a-b\right|\leq c_{1}\leq a+b,}$

jedoch ist ${\displaystyle c_{2}>a+b}$.

In einem normierten Raum ${\displaystyle \left(X,\|{\cdot }\|\right)}$ wird die Dreiecksungleichung in der Form

${\displaystyle \|x+y\|\leq \|x\|+\|y\|}$

als eine der Eigenschaften gefordert, die die Norm für alle ${\displaystyle x,y\in X\;}$erfüllen muss. Insbesondere folgt auch hier

${\displaystyle {\Big |}\|x\|-\|y\|{\Big |}\leq \|x\pm y\|\leq \|x\|+\|y\|}$

sowie

${\displaystyle \left\|\sum _{i=1}^{n}x_{i}\right\|\leq \sum _{i=1}^{n}\|x_{i}\|}$ für alle ${\displaystyle x_{i}\in X\;}$.

Im Spezialfall der L^p-Räume wird die Dreiecksungleichung Minkowski-Ungleichung genannt und mittels der Hölderschen Ungleichung bewiesen.

In einem metrischen Raum ${\displaystyle \left(X,d\right)}$ wird als Axiom für die abstrakte Abstandsfunktion verlangt, dass die Dreiecksungleichung in der Form

${\displaystyle d(x,y)\leq d(x,z)+d(z,y)}$

für alle ${\displaystyle x,y,z\in X}$ erfüllt ist. In jedem metrischen Raum gilt also per Definition die Dreiecksungleichung. Daraus lässt sich ableiten, dass in einem metrischen Raum auch die umgekehrte Dreiecksungleichung

${\displaystyle \left|d(x,z)-d(z,y)\right|\leq d(x,y)}$

für alle ${\displaystyle x,y,z\in X}$ gilt. Außerdem gilt für beliebige ${\displaystyle x_{i}\in X\;}$ die Ungleichung

${\displaystyle d(x_{0},x_{n})\leq \sum _{i=1}^{n}d(x_{i-1},x_{i})}$.

• Ungleichungen in Vierecken

1. ↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 18
2. ↑ Canadian Mathematical Olympiad 1969 Problem 3, veröffentlicht von der Canadian Mathematical Society
3. ↑ Harro Heuser: Lehrbuch der Analysis, Teil 1. 8. Auflage. B. G. Teubner, Stuttgart 1990, ISBN 3-519-12231-6. Satz 85.1
4. ↑ Walter Rudin: Real and Complex Analysis. MacGraw-Hill, 1986, ISBN 0-07-100276-6. Theorem 1.33