Feuerbachkreis – Wikipedia

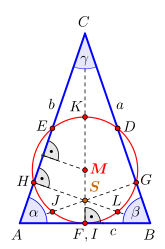
Der Feuerbachkreis, auch Feuerbachscher Kreis oder Neun-Punkte-Kreis ist ein besonderer Kreis im Dreieck, der nach Karl Wilhelm Feuerbach benannt ist. Auf ihm liegen neun ausgezeichnete Punkte:
- die Mittelpunkte der Seiten (D, E, F);
- die Fußpunkte der Höhen (G, H, I);
- die Mittelpunkte der oberen Höhenabschnitte (J, L, K) (das sind die Mittelpunkte der Strecken zwischen jeweils einer Dreiecksecke und dem Höhenschnittpunkt S des Dreiecks ABC).[1]
Sonderfälle
[Bearbeiten | Quelltext bearbeiten]- Der Feuerbachkreis geht genau dann durch eine Ecke des Dreiecks (nämlich den Scheitel des rechten Winkels), wenn das Dreieck (Bild 1) rechtwinklig ist.
- Der Feuerbachkreis berührt genau dann eine Dreiecksseite (nämlich die Basis), wenn das Dreieck (Bild 2) gleichschenklig ist.
- Der Feuerbachkreis stimmt genau dann mit dem Inkreis überein, wenn das Dreieck (Bild 3) gleichseitig ist.
- Bild 1: Rechtwinkliges Dreieck mit Feuerbachkreis (rot), die neun Punkte verteilen sich hier auf fünf unterschiedliche Positionen
- Bild 2: Gleichschenkliges Dreieck mit Feuerbachkreis (rot), die neun Punkte verteilen sich hier auf acht unterschiedliche Positionen
- Bild 3: Gleichseitiges Dreieck mit Feuerbachkreis (rot) und Inkreis (grün), die neun Punkte verteilen sich hier auf sechs unterschiedliche Positionen
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]
- Der Feuerbachkreis berührt den Inkreis des Dreiecks einschließend und die drei Ankreise des Dreiecks ausschließend, diese Eigenschaft wird auch als der Satz von Feuerbach bezeichnet. Der Punkt, in dem sich Feuerbachkreis und Inkreis berühren, wird Feuerbachpunkt des Dreiecks genannt. (Vorsicht: Manche, meist deutsche, Autoren bezeichnen den Mittelpunkt des Feuerbachkreises als „Feuerbachpunkt“ und dementsprechend die Existenz des Feuerbachkreises mit den in der Einleitung beschriebenen Eigenschaften als Satz von Feuerbach, siehe dazu z. B. Schupp)
- Der Mittelpunkt des Feuerbachkreises liegt genau in der Mitte zwischen Höhenschnittpunkt und Umkreismittelpunkt, also auch auf der eulerschen Geraden.[2]
- Der Radius des Feuerbachkreises ist halb so groß wie der Umkreisradius des Dreieckes.[2]

Feuerbachkreis und Umkreis - Der Feuerbachkreis halbiert die Strecke zwischen dem Höhenschnittpunkt und einem beliebigen Punkt auf dem Umkreis.
- Geht eine gleichseitige (rechtwinklige) Hyperbel durch die Ecken eines Dreiecks, dann liegt ihr Mittelpunkt auf dem Feuerbachkreis.
- Der Mittelpunkt der Kiepert-Hyperbel liegt auf dem Feuerbachkreis.[3]
- Der Umkreis eines Dreiecks ist der Feuerbachkreis des von den zugehörigen Ankreismittelpunkten induzierten Co-Dreiecks. (Die Winkelhalbierenden des ursprünglichen Dreiecks sind die Höhen des Co-Dreiecks. Die Lote von den Ankreismittelpunkten auf die Seiten des ursprünglichen Dreiecks treffen sich in einem Punkt, dem Umkreismittelpunkt des Co-Dreiecks. In der Mitte zwischen Co-Dreieck-Höhenschnittpunkt [= Inkreismittelpunkt des ursprünglichen Dreiecks] und Co-Dreieck-Umkreismittelpunkt liegt der Umkreismittelpunkt des ursprünglichen Dreiecks.)

- Die 4 Umkreise um Mittendreieck ([und Höhenfußpunktdreieck] Feuerbach-Kreis), Nagel-Dreieck (Kreis durch die Berührpunkte der Ankreise), Gergonne-Dreieck (Inkreis) und Winkelhalbierenden-Fußpunktdreieck haben einen Punkt gemeinsam, den Feuerbach-Punkt.
Koordinaten
[Bearbeiten | Quelltext bearbeiten]Die trilinearen Koordinaten des Feuerbach-Mittelpunkts () sind (gleichwertig)
- oder
- .[4]
Die baryzentrischen Koordinaten von sind (gleichwertig)
- oder
- .[4]
Die trilinearen Koordinaten des Feuerbach-Punkts () sind (gleichwertig)
- oder
- .[5]
Die baryzentrischen Koordinaten von sind
- .[5]
Dabei sind die Seitenlängen des Dreiecks und die Größen der Innenwinkel.
Geschichte
[Bearbeiten | Quelltext bearbeiten]
In Deutschland hat sich statt des Namens Neunpunktekreis der Name Feuerbachkreis eingebürgert. Grund dafür ist der von Feuerbach stammende, relativ schwierige Beweis, dass dieser Kreis den Inkreis und die Ankreise berührt. In der übrigen Welt sagt man meistens Neunpunktekreis. Es ist auch die Bezeichnung Eulerkreis verbreitet, denn dass die sechs Punkte D bis I auf einem Kreis liegen, zeigte schon Leonhard Euler 1765, (s. Bild 1–3).[6] 1821 bewiesen Charles Julien Brianchon und Jean Victor Poncelet, dass diese sechs Punkte und noch drei weitere Punkte auf dem Kreis liegen, die Mittelpunkte der oberen Höhenabschnitte J, K, L. Feuerbach bewies 1822, dass der ursprünglich durch die Fußpunkte G, H, I gehende Kreis die In- und Ankreise berührte und außerdem durch die Seitenmitten E, F, D geht.[7] Die übrigen drei Punkte J, K, L des Feuerbachkreises erwähnt er nicht. Wegen der sechs Punkte D bis I heißt er manchmal auch Sechspunktekreis. Der Feuerbachkreis wird auch manchmal nach Olry Terquem benannt, der selbst dafür 1842 den Begriff Neunpunktekreis prägte und einen analytischen Beweis des Satzes von Feuerbach über die In- und Ankreise gab (und die zusätzlichen drei Punkte wieder entdeckte). Eine weitere Wiederentdeckung des Neunpunktekreises geschah durch Jakob Steiner 1828 und T. S. Davies 1827.[8] J. S. MacKay fand 1892 in seinem Aufsatz zur Geschichte des Neunpunktekreises auch einige englische Autoren, die vor 1821 zur Geschichte des Feuerbachkreises beitrugen.
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3, S. 164–167 (Auszug (Google))
- Charles S. Ogilvy: Unterhaltsame Geometrie („Excursions in geometry“, 1969). 3. Auflage. Vieweg Verlag, Braunschweig 1984, ISBN 3-528-28314-9.
- Hans Schupp: Elementargeometrie. Schöningh, Paderborn 1977, ISBN 3-506-99189-2 (Uni-Taschenbücher 669 Mathematik), S. 133–135
- John Sturgeon MacKay: History of the Nine Point Circle. Proceedings of the Edinburgh Mathematical Society, Band 11, 1892, S. 19–61.[9][10]
- Stefan Götz, Franz Hofbauer: Ein einfacher Beweis für den Satz von Feuerbach mit koordinatenfreien Vektoren. Mathematische Semesterberichte (Springer), Band 65, 2018, S. 107–119
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Landesbildungsserver-BW – Informationen zum Feuerbachkreis mit Beweisen, Folgerungen und Hinweisen
- Feuerbachkreis – interaktive Illustration in GeoGebra
- Feuerbachkreis auf thema-mathematik.at (Wiki mit mehreren Grafiken und GeoGebra-Dateien)
- Darij Grinberg: Feuerbachkreis mit sehr viel Information aus dem Umfeld (PDF; 190 kB) – ein sehr ausführliches Papier zum Feuerbachkreis mit sehr vielen Sätzen aus dem Umfeld. Sehr viele Beweise, auch ein Beweis zum Satz von Feuerbach.
- Eric W. Weisstein: Nine Point Circle. In: MathWorld (englisch).
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer, Berlin Heidelberg New York 2007, ISBN 978-3-540-49327-3, S. 166.
- ↑ a b Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer, Berlin Heidelberg New York 2007, ISBN 978-3-540-49327-3, S. 165.
- ↑ Clark Kimberling: Enyclopedia of Triangle Centers, X(115). Abgerufen am 25. Januar 2025 (englisch).
- ↑ a b Clark Kimberling: Enyclopedia of Triangle Centers, X(5). Abgerufen am 25. Januar 2025 (englisch).
- ↑ a b Clark Kimberling: Enyclopedia of Triangle Centers, X(11). Abgerufen am 25. Januar 2025 (englisch).
- ↑ Eric Weisstein, Nine point circle, Mathworld
- ↑ Meyer, Berkhan, Neuere Dreiecksgeometrie, in: Enzyklopädie der mathematischen Wissenschaften, Band 3-1-2, 1914, S. 1258
- ↑ Webseite zur Geschichte nach J. MacKay (Proc. Edinburgh Math. Society, Band 11, 1892, S. 19–57)
- ↑ Jim Wilson, History of the nine point circle, University of Georgia. Er bezieht sich auf MacKay
- ↑ cambridge.org


 French
French Deutsch
Deutsch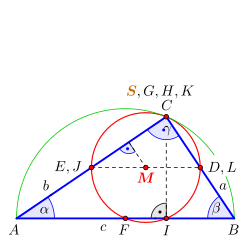



![{\displaystyle bc\left[a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}\right]:ca\left[b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}\right]:ab\left[c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7ea2eb56e01171f5d32ce3a14583c8432f9b4dc)

![{\displaystyle \left[a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}\right]:\left[b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}\right]:\left[c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e071dc2d5e74db0320c84beaf04d97f8fc8eba76)



![{\displaystyle \left[1-\cos(\beta -\gamma )\right]:\left[1-\cos(\gamma -\alpha )\right]:\left[1-\cos(\alpha -\beta )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6eaf09a9529d328d20799bfc46b8549579ae372c)


