Hjulström-Diagramm – Wikipedia

Das Hjulström-Diagramm beschreibt die Stabilität von klastischen Sedimentablagerungen oder anderen Partikelakkumulationen (z. B. Regolith bzw. Boden) hinsichtlich der Fließgeschwindigkeit von Wasser. Es ist ein doppellogarithmisches empirisch gewonnenes Diagramm mit der mittleren Korngröße d auf der Abszisse und der mittleren Geschwindigkeit v auf der Ordinate. Das Hjulström-Diagramm zeigt somit den Zusammenhang zwischen Korngröße und Fließgeschwindigkeit. Es ist nach dem schwedischen Geographen Filip Hjulström (1902–1982) benannt.

Das Diagramm ist durch zwei Kurven, die sogenannten Grenzgeschwindigkeiten oder kritischen Geschwindigkeiten, in drei Felder geteilt:

• Erosion,
• Transport und
• Sedimentation

Grundsätzlich folgt aus dem Diagramm:

• Die Fließgeschwindigkeit v, die für die Erosion eines Korns bzw. Partikels nötig ist, ist stets größer als die Fließgeschwindigkeit, die nötig ist, diesen Partikel nicht zur Ablagerung kommen zu lassen (in Suspension zu halten).
• Je höher die Fließgeschwindigkeit, desto größer kann das transportierte Korn (d) sein (v ist direkt proportional zu d)
• Je kleiner der Korndurchmesser d, umso geringer ist die notwendige Fließgeschwindigkeit v, um Erosion herbeizuführen. Aber: Unter einem Korndurchmesser von 0,3 mm nimmt die Kohäsion zwischen den Partikeln zu und damit die für die Erosion erforderliche Fließgeschwindigkeit. Sobald solche Partikel aber erodiert sind, bleiben sie umso länger in Suspension. Das Feld „Transport“ ist für die kleinsten Korngrößen daher am größten.

Zu beachten ist, dass mittlere Fließgeschwindigkeit und mittlere Korngröße nur Ersatzgrößen für alle auf ein Partikel wirkenden Kräfte sind. Wichtige Einflussfaktoren auf die Stabilität von Partikelakkumulationen sind die Rauigkeit der Oberfläche, die Kohäsion zwischen den einzelnen Partikeln und die Gewichtskraft eines einzelnen Partikels. Alle diese Faktoren sind jedoch wenigstens teilweise durch den Hulström’schen Ansatz berücksichtigt, denn die Oberflächenrauigkeit und die Gewichtskraft korrelieren positiv mit der Korngröße, die Kohäsion korreliert negativ mit der Korngröße. Das heißt, auch wenn es allein nicht alle exogenen Prozesse unter Mitwirkung flüssigen Wassers erklären kann, so spiegelt das Diagramm dennoch relativ genau die beobachteten Abhängigkeiten der Erosion, des Transports und der Sedimentation von Fließgeschwindigkeit und Korngröße wieder.

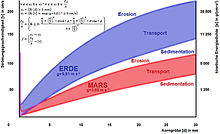
Das „Zasada-Diagramm“ illustriert, wie auch das Hjulström-Diagramm, den Zusammenhang zwischen mittlerer Korngröße und durchschnittlicher Fließgeschwindigkeit hinsichtlich der Prozesse Erosion, Transport und Sedimentation, jedoch in Abhängigkeit von der Gravitation. Entwickelt wurde es für den Vergleich der Transport- und Sedimentationsbedingungen auf Erde und Mars. Der mathematische Ansatz, der dem Diagramm zugrunde liegt, lässt sich zwar prinzipiell auf alle übrigen terrestrischen Planeten extrapolieren, jedoch ist bislang nicht nachgewiesen, dass oberflächenformende Prozesse durch flüssiges Wasser überhaupt noch auf weiteren Objekten im Sonnensystem auftraten oder sogar rezent auftreten.

Das Zasada-Diagramm verdeutlicht, dass die landschaftsprägenden Erosions- und Sedimentationsprozesse stark von der Gravitation eines Planeten beeinflusst werden: Ähnliche Strukturen auf Erde und Mars gehen auf jeweils unterschiedliche Strömungsgeschwindigkeiten und Durchflussraten während der Ablagerung zurück. Dies lässt Rückschlüsse auf die geologische Geschichte des Mars zu: Weil die Strömungsgeschwindigkeit auf dem Mars geringer sein darf, um gleiche Strukturen wie auf der Erde zu erschaffen, und weil die Strömungsgeschwindigkeit generell direkt proportional der Durchflussrate ist, besteht die Möglichkeit, dass der Mars in seiner Vergangenheit weniger Wasser besaß, als es seine heutigen Stromtäler und Delta-Strukturen zunächst vermuten lassen.

Das Shields-Diagramm beschreibt die Übergangszone zwischen Ruhe und Bewegung von Sand und Kies in einem Flussbett. Im Original-Shields-Diagramm ist dabei die kritische Strömungsintensität über die sedimentologische Reynoldszahl aufgetragen.

Im modifizierten Shields-Diagramm ist die kritische Strömungsintensität über der dimensionslosen Korngröße aufgetragen.

• Frank Ahnert: Einführung in die Geomorphologie (= UTB für Wissenschaft. Geowissenschaften, Geologie. Band 8103). 4. Auflage. Ulmer, Stuttgart 2009, ISBN 978-3-8001-2907-2. 
• Filip Hjulström: Studies of the morphological activity of rivers as illustrated by the River Fyris. In: Bulletin of the Geological Institute University of Uppsala, 25, Uppsala 1935, S. 221–527
• David Knighton: Fluvial Forms and Processes. A new Perspective. Completely revised and updated edition. Arnold, London u. a. 1998, ISBN 0-340-66313-8. 
• Luna B. Leopold, M. Gordon Wolman, John P. Miller: Fluvial Processes in Geomorphology. Unabridged and unaltered Republication of the Work first published by W. H. Freeman and Company, San Francisco, in 1964. Dover Publishing, Mineola NY 1995, ISBN 0-486-68588-8. 
• Hans-Joachim Vollmers: Kritische Geschwindigkeiten und Schubspannungen. In: Hans-Burkhard Horlacher (Hrsg.): Belastung, Stabilisierung und Befestigung von Sohlen und Böschungen wasserbaulicher Anlagen. Vorträge zum Wasserbaukolloquium vom 16.03. bis 17.03.2000 (= Dresdner Wasserbauliche Mitteilungen). H. 18. TU Dresden – Institut für Wasserbau und Technische Hydromechanik, Dresden 2000, ISBN 3-86005-243-8, S. 45–56 (baw.de [PDF; 3,1 MB]). 
• Patrick Zasada: Sortierung fluviatiler Sedimente auf terrestrischen Planeten in Abhängigkeit zur Gravitation. In: Zeitschrift für Geologische Wissenschaften. Band 41/42, Nr. 3, 2013, S. 167–183 (online). 
• Harald Zepp: Geomorphologie. Eine Einführung (= Grundriss allgemeine Geographie = UTB Geographie. Band 2164). 4., aktualisierte und erweiterte Auflage. Schöningh, Paderborn u. a. 2008, ISBN 978-3-506-97013-8. 

• Flashanimation des Hjulström-Diagramms
• Hjulström-Diagramm im Spektrum Lexikon der Geowissenschaften (Online-Version)